Je kan een aantal mogelijke oplossingen uitproberen. Misschien kan je zelfs het aantal mogelijke oplossingen beperken. Dan kan je best een gokje wagen en daarna proberen te bewijzen dat jouw voorstel tot oplossing de goede is.

Bepaal de volgende term in de rij:

$-1,-1,1,5,11,19,29,\cdots$

Het is zeker geen rekenkundige rij. Een eerste graadsveelterm zal dus niet kunnen om de algemene term van de rij te bepalen. Het is ook geen meetkundige rij , dus ook een exponentiële functie zal niet volstaan.
Proberen we even met een tweedegraadsfunctie. Dus een uitdrukking van de vorm 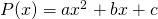$P(x)=ax^2+bx+c$ . Proberen we nu de waarden van de onbekenden $a,b$ en $c$ te vinden.
Uit 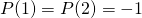$P(1)=P(2)=-1$ en $P(3)=1$ vinden we een stelsel:
$\left\{ \begin{array}{l}a+b+c=-1 \\ 4a+2b+c=-1\\9a+3b+c=1 \end{array} \right$

.
De oplossing van het stelsel is 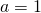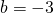$a=1$ , $b=-3$ e, $c=1$ .
De vraag is natuurlijk of onze gok goed was! Voldoen de andere termen van de rij ook aan het voorschrift?
Nu is: $P(4)=5$ , $P(5)=11$ , $P(6)=19$ , $P(7)=29$ .
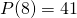De volgende term in de rij is $P(8)=41$ .

Wiskunde is leuk

Waag eens een gokje

Bepaal de volgende term in de rij:

$-1,-1,1,5,11,19,29,\cdots$