De tekenregel werd voor het eerst genoemd in het werk ‘La géometrie’ van René Descartes (1596-1650). Het gaat over veeltermen met reële coëfficiënten en we zijn geïnteresseerd in het aantal positieve nulwaarden. Veronderstellen we voor de rest van deze tekst dat de coëfficiënt van gelijk is aan 1, dat de constante term niet nul is  en dat de veelterm geordend is naar afnemende machten van x.

Het fundamenteel theorema van de algebra zegt dat een veelterm van graad n steeds n nulwaarden heeft in . Meestal zijn we niet in staat deze nulwaarden te vinden. Toch kunnen we informatie vinden over het aantal positieve reële nulwaarden ( p) en het aantal negatieve nulwaarden (n). Bestudeer hiervoor het aantal teken veranderingen in de rij van tekens van de niet nul zijnde coëfficiënten van de gegeven veelterm P(x):

• De waarde p heeft dezelfde pariteit als het aantal  tekenveranderingen.
• De waarde p is kleiner of gelijk aan het aantal tekenveranderingen.
• Om n te bepalen bepalen we p voor de veelterm P(-x).

Een voorbeeld: .

• Er zijn 5 tekenveranderingen.
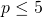• en p is oneven, dus p = 1, 3 of 5
• . Er is 1 tekenverandering dus .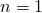
• Narekenen geeft als nulwaarden: 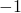en 2 met multipliciteit 2 en 3.