Tag archieven: zeshoek

Opgave 40

Geplaatst op door

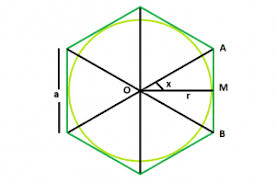
Een convexe zeshoek is ingeschreven in een cirkel met straal r. Twee zijden van deze zeshoek hebben als lengte 7 eenheden , terwijl de vier overige als lengte 20 eenheden hebben. Bepaal de straal van de cirkel.

Antwoord

Sangaku 6

Geplaatst op door

Antwoord

Pi met wortels

Geplaatst op door

Hoe kan je pi benaderen door middel van wortels? Bekijk volgende  mogelijkheid: de oppervlakte van een cirkel met straal 1 benaderen we door het gemiddelde te nemen van de oppervlaktes van een ingeschreven regelmatige achthoek en een omgeschreven regelmatige zeshoek.

  • Neem een omgeschreven zeshoek :
    om de oppervlakte te berekenen nemen we zes keer de oppervlakte van OAB. De hoogte OM van die driehoek is 1. De basis AB is 2*\tan 30^\circ=\frac{2\sqrt{3}}{3}. Bijgevolg is de oppervlakte van de zeshoek gelijk aan 2\sqrt{3}.
  • Neem vervolgens een ingeschreven regelmatige achthoek:
    de oppervlakte is gelijk aan acht keer de oppervlakte van driehoek OAB. De oppervlakte van die driehoek is gelijk aan \frac{1}{2}*1*1*\sin 45^\circ=\frac{\sqrt{2}}{4}, zodat de oppervlakte van de achthoek gelijk is aan 2\sqrt{2}.
  • Het gemiddelde van die twee oppervlaktes is dan \sqrt{2}+\sqrt{3}.
  • Aldus is \pi \approx \sqrt{2}+\sqrt{3}\approx 3.14626436994