Tag archieven: wiskundige raadsels

Nog een raadseltje

Geplaatst op door

De pastoor geeft zijn parochieassistente een probleempje om op te lossen: “Er zijn drie parochianen waarvan het product van de ouderdommen gelijk is aan 2450. De som van hun ouderdommen is het dubbel van jouw leeftijd.” De assistente zegt: “Ik weet het nog niet.” Dan zegt de pastoor: “De drie parochianen zijn alle drie jonger dan ik.’ “Nu weet ik het,” roept de parochieassistente. Welke zijn de leeftijden van de drie parochianen?

Antwoord

  • Noem de parochianen a, b en c en de assistente x. We gaan ervan uit dat de leeftijden allemaal natuurlijke getallen zijn.
  • 2450=2*5*5*7*7. We maken een tabel van de mogelijkheden waarvoor abc = 2450 en berekenen tegelijkertijd ook x ( de helft van  a + b + c). We gebruiken enkel ‘echte’ leeftijden, dus niet bvb 1225 of zo.

  •     \[\begin{array}{c|c|c|c} a&b&c&x\\ \hline \\2&25&49&38\\2&35&35&36\\5&5&98&54\\5&7&70&41\\5&10&49&32\\5&14&35&27\\7&7&50&32\\7&10&35&26\\7&14&25&23 \end{array}\]

  • De assistente weet uiteraard haar eigen leeftijd en omdat ze het antwoord niet kan geven op de haar gestelde vraag, moet haar leeftijd twee of meer keer voorkomen; dit gebeurt enkel bij (a,b,c,x)=(5,10,49,32)=(7,7,50,32)).
  • Als de leeftijd van de pastoor 51 of meer is, dan blijven bieden mogelijkheden bestaan en zou ze het antwoord dus niet kennen. Als hij jonger is dan 50 voldoen geen van de twee mogelijkheden. Dus is de pastoor 50 jaar en voldoet enkel 5,10 en 49 als leeftijden van de drie parochianen.

Hoeden en logica

Geplaatst op door

Drie personen (A,B en C) elk met een hoed met daarop een natuurlijk getal, verschillend van 0. Iedereen ziet de nummers op de hoed van de anderen, maar niet zijn eigen nummer. Wel is 1 nummer de som van de andere twee .

A: ik kan niet weten wat mijn nummer is.
B: ik kan niet weten wat mijn nummer is.
C: ik kan niet weten wat mijn nummer is.
A: mijn nummer is 50

Wat zijn de andere twee nummers?

  • B en C kunnen niet hetzelfde nummer hebben anders zou A weten wat zijn nummer is. idem voor B en C, dus de combinaties (2k,k,k), (k,2k,k) en (k,k,2k) zijn zeker onmogelijk.
  • Omdat B zijn nummer niet weet kan ook (2k,3k,k) niet. Want als B k en 2k ziet, zijn er voor hem/haar 2 mogelijkheden : k of 3k. Maar k kan het niet zijn, want anders had A zijn nummer al geweten. Bijgevolg zou B weten wat zijn nummer is. Eenzelfde redenering kunnen we voor C voeren. Dus zijn ook volgende combinaties onmogelijk: (2k,k,3k), (k,2k,3k),  (2k,3k,k) en (k,3k,2k).
  • C weet zijn nummer ook niet. Dus kan (2k,3k,5k). Want als C 2k en 3k ziet staan heeft hij/zij als mogelijkheden k en 5k. Maar uit vorig punt weten we al dat k niet kan , dus C zou zijn mummer weten! Idem voor de combinatie (3k,2k,5k).
  • Nu is A terug aan de beurt. Hij/zij weet zijn nummer in de gevallen (3k,2k,k), (4k,3k,k), (3k,k,2k),(4k,k,3k), (5k,2k,3k) en (8k,3k,5k). Maar hij zegt dat het 50 is, dus blijft enkel (5k,2k,3k) als echte mogelijkheid. De getallen zijn dus 50, 20 en 30, voor respectievelijk A,B en C.

Puzzels door de eeuwen heen

Geplaatst op door

Puzzels, raadsels, denkspelen hebben de mensheid altijd al gefascineerd Archeologische opgravingen hebben hun aanwezigheid kunnen vaststellen bij vrijwel alle beschavingen. Uit de verre oudheid  kennen we onder andere het koningsspel van Ur en het Senet bordspel uit Egypte:

 

 

 

 

 

 

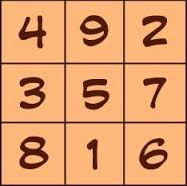
Oorspronkelijk was de functie van die denkspelen eerder mythisch-religieus. Bordspelen konden aanwijzingen geven over het verloop van een oorlog. Via tekens kon de Godheid communiceren met de mensheid. Vooral de getallen hadden dan een magische betekenis. Denk maar aan het magische vierkant van Lo Shu. Voor de Chinezen waren de oneven getallen mannelijk en was het kruis het symbool van mannelijkheid en goddelijkheid.

In de loop  van de geschiedenis is de klemtoon evenwel verschoven en is men het spel meer gaan bekijken als een aangenaam tijdverdrijf. De spelletjes waren fascinerend omwille van de uitdaging die er in school. Ook beroemde wiskundigen hebben zich ermee bezig gehouden: Alcuïnus met het probleem van de wolf, de geit en de kool; Fibonacci met het konijnenprobleem, Gauss met de verplaatsing van de dames op een schaakbord,…

Nog later werden vele intellectuele spelletjes uit de recreatieve sfeer gehaald  en werden onderworpen aan een grondige wiskundige analyse. Neem het voorbeeld van de 7 bruggen van Königsberg met de grafentheorie of het vierkleurenprobleem. De banden tussen recreatieve en ernstige wiskunde werden aangehaald en ingewikkelde wiskundige technieken werden gebruikt bij de analyse van schijnbaar eenvoudige problemen.