Neem een willekeurig getal uit een grote verzameling  natuurlijke getallen, verschillend van 0. Hoe groot is de kans dat het begincijfer een 1 is ? Of een 2? Uiteraard verwachten we dat elk cijfer evenveel kans heeft om als begincijfer op te treden.

Neem de proef op de som en neem als voorbeeld  de verzameling beurskoersen op de beurspagina van de krant van vandaag. Natuurlijk zullen sommige van die getallen beginnen met een 1, maar aanzienlijk minder dan de getallen die met een 1 beginnen. Het begincijfer 3 is nog zeldzamer en uiteindelijk vormen de getallen die beginnen met een 9 een kleine minderheid.

Al in 1881 observeerde Simon Newcomb dit fenomeen. Deze wiskundige astronoom ontleende een veelgebruikt boekje met logaritmetafels uit de bibliotheek en hij vond dat vooral de pagina’s met getallen met begincijfer 1 er verfrommeld uitzagen. Hij publiceerde zelfs een artikel waarin hij de volgende formule voorstelde om de kans P(n) te berekenen op begincijfer n:

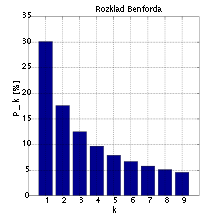
Als je deze formule gebruikt dan vindt je ongeveer 30% kans hebt dat het begincijfer een 1 is. In een diagram :

In 1938 kwam de natuurkundige Frank Bedford tot dezelfde bevinding onafhankelijk van Newcomb. Het verschil was dat hij zich baseerde op meer dan twintigduizend getallen, willekeurig geplukt uit kranten en edities van Readers Digest. Sinds zijn publicatie refereert iedereen naar bovenstaande formule als de formule van Bedford.

Maar een wet die niet bewezen wordt; neemt een folkloristische plaats in naast wetten zoals de wet van Murphy. Gelukkig heeft de kanstheoreticus Ted Hill in 1996 een formeel wiskundig bewijs gevonden voor de wet van Bedford. De cruciale voorwaarde in zijn bewijs is dat de getallen willekeurig uit verschillende kansverdelingen gekozen worden, met dus een variërend bereik