vijfhoeken | Wiskunde is leuk

Deze sangaku werd beschreven op een tablet van de Miyagi Prefecture uit 1912

Antwoord

We gaan op zoek naar de lengte van de schuine zijde van de groene rechthoekige driehoeken. Noteer de zijde van de regelmatige vijfhoek door a.
We leggen volgende notatie vast:
De scherpe hoek van de groene driehoek, die grenst aan de vijfhoek is $36^\circ$ (de helft van het supplement van de hoek van een vijfhoek, en die is $108^\circ$ ).
Driehoek $A_3A_4A_5$ is gelijkbenig en dus zijn de basishoeken elk $36^\circ$ . Volgens de cosinusregel is $l^2=2a^2(1-\cos 108^\circ)=4a^2\sin^2 72^\circ=4a^2\cos36^\circ$
Hieruit volgt dat $l=2a\cos 36^\circ$ .
In driehoek $A_3MA_5$ is $h=l\sin 72^\circ$ . Samen met vorig resultaat geeft dit dat $h=2a\cos 35^\circ \sin 72^\circ$ .
In driehoek $A_3MP$ is $c=\frac{h}{\cos 54^\circ}=\frac{2a\cos 35^\circ \sin 72^\circ}{\cos 54^\circ}$ .
Tenslotte, in driehoek $A_3PH$ is $t=\frac{c}{\cos 36^\circ}$ .
Hierin kunnen we c invullen en krijgen we, omdat $\cos 36^\circ=\frac{1+\sqrt{5}}{4}$ :
$t=a(1+\sqrt{5})$

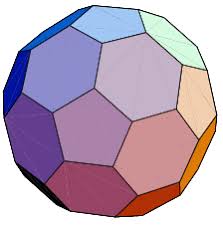
Op een voetbal komt een netwerk van bogen voor, die de oppervlakte van de bal verdelen in een aantal gebieden. Sommige van die gebieden worden door vijf bogen begrensd en zijn dus vijfhoekig van vorm; de rest van de gebieden is zeshoekig. Bij elk knooppunt van het netwerk komen drie gebieden samen; twee daarvan zijn zeshoekig en het derde is vijfhoekig. De vijfhoekige gebieden zijn zwart en de zeshoekige zijn wit. Elk vijfhoekig gebied omgeven wordt door een krans van vijf zeshoekige gebieden.

Noemen we het aantal knooppunten V ( vertrices), E het aantal bogen (edges) en F het aantal gebieden (faces). Euler zegt dat

$V-E+F=2$

Stel x het aantal vijfhoeken en y het aantal zeshoeken. Er zijn dus 5x , maar ook 6y knooppunten ( want in elk hoekpunt komen 2 zeshoeken samen). Bijgevolg is $y=\frac{5}{3}x$ .
Alle vijfhoeken en zeshoeken hebben samen $5x + 6y = 5x + 10x= 15x$ zijden. Bij elke boog van het netwerken vallen twee zijden samen dus $E=\frac{15}{2}x$ .
Het aantal gebieden wordt gegeven door $F=x+y=\frac{8}{3}x$ .