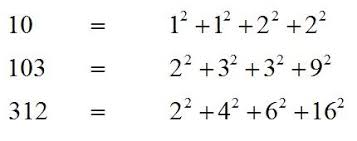Tag archieven: vier kwadraten stelling

Vierkwadraten stelling

Geplaatst op door

Elk priemgetal, gelijk aan 1 modulo 4, kan geschreven  worden als som van twee kwadraten. Dat een getal als som van twee kwadraten
geschreven kan worden is niet vanzelfsprekend. Bij een getal dat 3 (mod 4) is kan dat bijvoorbeeld niet. Daarentegen bleek dat wel elk getal getal te schrijven is als som van vier kwadraten.

Elk positief geheel getal kan geschreven worden als som van 4 kwadraten van gehele getallen.

    \[n=x_1^2+x_2^2+x_3^2+x_4^2\]

Deze stelling was al gekend door Diophantus; Euler heeft 40 jaar gezocht naar een bewijs ervan, maar het was Joseph-Louis Lagrange ( 1736 – 1813)  die in 1772 het eerste bewijs formuleerde.

Het kan zelfs in veel gevallen met drie kwadraten. Legendre ( 1752 – 1833) beweerde dan elk getal, tenzij van de vorm 4^k(8m+7) , te schrijven is als som van drie kwadraten.

Er bestaat zelfs een mogelijkheid  om  het totaal aantal manieren  te berekenen, waarop een gegeven positief geheel getal n  kan worden geschreven als de som van vier kwadraten. Als n oneven is moet je 8 keer de som van zijn delers nemen en als n even is 24 keer de som van zijn oneven delers. Merk hierbij op dat (x_1,x_2,x_3,x_4) geordend is en dat we gehele oplossingen zoeken ; dus ook rekening houden met negatieve getallen.