Je mag maximaal 5 keer werpen met een dobbelsteen. Je mag na elke beurt stoppen, en je krijgt het aantal ogen van de laatste worp uitbetaald in goudstaven. Vind een strategie waarmee je gemiddeld het meest aantal goudstaven wint.


Als je 1 gooit, is het duidelijk ongunstig om te stoppen. En als je een 6 gooit, dan kan je dat niet verder verbeteren en is het logisch dat je dan stopt. Maar wat doe je als je iets anders gooit? Een handige manier om daar achter te komen is het volgende: als je de eerste van je 5 worpen afkeurt en besluit verder te gaan om hogere ogen te gooien, kom je eigenlijk in een nieuw spel terecht : een spel met 4 worpen met dezelfde spelregels. Zo doorredenerend kom je uiteindelijk in een spel terecht waarvan je de strategie al kent: je mag één keer gooien en je enige optie is te stoppen.
Hoeveel goudstaven zou die ene keer gooien gemiddeld opleveren? Vermits elke waarde van de dobbelsteen even waarschijnlijk geworpen wordt is dat
![Rendered by QuickLaTeX.com \[\frac{1}{6}(1+2+3+4+5+6)=3,5\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-b8f771f08c1dbb1fb7fd770bdbba3d97_l3.png?media=1678572382)
. Deze informatie helpt je bij het vorige spel: het spel met 2 worpen. Je wilt beter doen dan het gemiddelde. Dus als de eerste worp beter is dan 3,5 dan stop je en anders ga je door. Je kan in je eerste worp 4,5 of 6 goudstaven winnen elk met kans 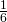 . In het andere geval ga je door en win je gemiddeld 3,5 goudstaven. De totale gemiddelde winst van dit spel met 2 worpen is dus
. In het andere geval ga je door en win je gemiddeld 3,5 goudstaven. De totale gemiddelde winst van dit spel met 2 worpen is dus
![Rendered by QuickLaTeX.com \[\frac{1}{6}(4+5+6)+\frac{1}{2}.3,5=4,25.\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-393c20fb5c4b811ff9bee774d934b562_l3.png?media=1678572382)
Deze waarde kan je nu weer gebruiken in het spel met 3 worpen. Je stopt bij de eerste worp als je 5 of 6 (meer dan 4,25) gooit. anders ga je verder en stopt als je 4,5 of 6 gooit. Zo niet ga je nog 1 keer verder. De gemiddelde winst is nu:
![Rendered by QuickLaTeX.com \[\frac{1}{6}(5+6)+\frac{4}{6}\frac{1}{6}(4+5+6)+\frac{1}{2}3.5=4,66\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-7f4032d74d6c76489ff55b344703f9b7_l3.png?media=1678572382)
Verder redeneren geeft volgende strategie voor het 5 beurten spel: Bij de eerste drie keer gooien alleen stoppen als je 5 of 6 gooit, bij de vierde beurt als je 4,5 of 6 gooit en anders er een laatste beurt aan wagen. Stel  en
en 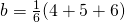 , dan is de gemiddelde winst:
, dan is de gemiddelde winst:
![Rendered by QuickLaTeX.com \[a+\frac{4}{6}a+\frac{4}{6}\frac{4}{6}a+\frac{4}{6}\frac{4}{6}\frac{4}{6}b+\frac{4}{6}\frac{4}{6}\frac{4}{6}\frac{1}{2}.3,5=5,12\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-61cbb922f37f18945caeb43493982d44_l3.png?media=1678572382)
Met de gegeven strategie verdien je uiteindelijk gemiddeld 5,12 goudstaven.
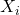 het aantal kaarten in de i-de groep. Dan geldt:
het aantal kaarten in de i-de groep. Dan geldt: ![Rendered by QuickLaTeX.com \[0 \leq X_i \leq 48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba2b507c09a658d2fe2ffcc7084a6ae9_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[X_1+X_2+X_3+X_4+X_5=48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-65cda2951fedf127f5d52d5aa6910813_l3.png?media=1678572382)
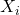 is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke
is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke 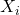 dezelfde zijn.
dezelfde zijn.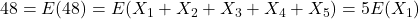 .
.![Rendered by QuickLaTeX.com \[E(X_1)=\frac{48}{5}=9,6\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-50f79ad0e630b542d93d616e003405ab_l3.png?media=1678572382)
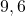 .
.




