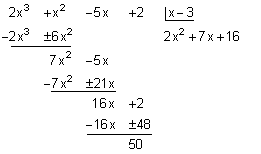Tag archieven: veeltermen

Uitdaging 3 en 4

Geplaatst op door

Voor welke waarden van k is x^3+y^3+z^3+kxyz deelbaar door x+y+z?

Antwoord

  • Als x^3+y^3+z^3+kxys deelbaar is door x+y+z, dan bestaat er een Q(x,y,z) zodat

        \[x^3+y^3+z^3+kxyz=(x+y+z)Q(x,y,z)\]

  • Vervang nu in beide leden x door 2, en y en z door -1, dan vind je 8-1-1+2k=0 of m.a.w. k=-3.

Een veelterm f(x)  met gehele coëfficiënten heeft oneven getalwaarden voor 0 en 1. Bewijs dat  f(x) geen gehele nulwaarden kan hebben.

Antwoord

  • Noteer de veelterm f(x)=a_nx^n+\cdots+a_1x+a_0.
  • Omdat f(0) oneven is moet a_0 een oneven getal zijn.
  • Omdat f(1) even is moet a_n+\cdots+a_1+a_0 ook oneven zijn.
  • Stel nu dat c een gehele nulwaarde is van f(x), dan is a_nc^n+\cdots+a_1c+a_0=0.
  • Als c even is dan is het linkerlid van deze ongelijkheid oneven en kan dus nooit nul zijn.
  • Als c oneven is, dan krijgen we modulo 2 dat a_n+\cdots+a_1+a_0 \equiv 0. Maar ook dat is onmogelijk want het linkerlid is oneven en kan dus nooit  nul zijn.
  • Dus heeft f(x) geen gehele nulwaarden.

Uitdaging 1 en 2

Geplaatst op door

Wat is de som der coëfficiënten van (3x^2-3x+1)^{200}.(x^2+x-3)^{2020}.

Antwoord

  • Zeker niet uitrekenen!
  • Probeer een eenvoudig voorbeeld: (x+2)^2. Uitgewerkt is dit x^2+4x+4. Als we x vervangen door 1 krijgen we de gevraagde som 1 + 4 + 4 = 9.
  • Vervang dus x door 1 voor het uitrekenen en we vinden dat voor onze opgave de gewenste som gelijk is aan (3-3+1) ^{200}.(1+1-3)^{2020}=1.

Toon aan dat \sqrt[n]{7} irrationaal is voor elk natuurlijk getal n groter dan 1

Antwoord

  • \sqrt[n]{7} is een oplossing van de vergelijking x^n-7=0.
  • Als \frac{p}{q} een rationale oplossing zou zijn van deze vergelijking moet p een deler zijn van 7 en q een deler van de coëfficiënt van x^n, dus 1.
  • De enige mogelijkheden zijn \pm1,\pm 7 en geen van deze 4 is een goede oplossing.
  • Er zijn dus geen rationale oplossingen bijgevolg is \sqrt[n]{7} steeds irrationaal.

Deelbaarheid bij veeltermen

Geplaatst op door

We geven enkelen eigenschappen in verband met deelbaarheid bij veeltermen. Deze eigenschappen lijken op de deelbaarheidseigenschappen bij gehele getallen:

  • Voor twee veeltermen f(x) en g(x) bestaat er een uniek quotiënt q(x) en een unieke rest r(x) zodat f(x) = q(x) . g(x) + r(x) met gr(r(x)) < gr (g(x)).
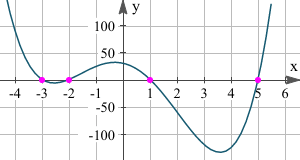
  • De rest van de deling van f(x) door x – a is f(a). Deze eigenschap noemen we de reststelling. Dit levert meteen een criterium voor deelbaarheid door veeltermen van de vorm x – a: de veelterm f(x) is deelbaar door x – a als f(a) = 0.
  • Als a en b verschillend zijn dan is f(x) deelbaar door (x – a)(x – b) als f(a) = f(b) = 0.
  • De veelterm f(x) is deelbaar door (x-a)^k als a een nulpunt is van f(x) en de eerste k – 1 afgeleiden van f(x). We spreken dan van een k- voudig nulpunt.
  • Er bestaan veeltermen die elkaar wederzijds delen, we noemen deze  toegevoegde elementen. Zo zijn alle reële getallen verschillend van 0 toegevoegd aan 1. De elementen toegevoegd aan 1 noemen we eenheden. Het is duidelijk dat toegevoegde elementen slechts verschillen van een factor gelijk aan een eenheid.
  • Zijn f(x) en g(x) van nul verschillende veeltermen dan bestaat er onder de toegevoegde elementen  van hun ggd (kgv) precies 1 waarvan de hoogste graadsterm coëfficiënt 1 heeft. Deze unieke veelterm wordt weleens dé ggd(kgv) van f(x) en g(x) genoemd.
  • Voor elk tweetal veeltermen f(x) en g(x) bestaan er veeltermen p(x) en q(x) zodat ggd( f(x) , g(x) ) = p(x) . f(x) + q(x) . g(x). Dit is de eigenschap van Bezout.
  • Een veelterm, verschillend van nul en van een eenheid, waarvan de enige delers eenheden of toegevoegde elementen zijn, noemen we een irreduciebele veelterm. Deze veeltermen zijn dus niet ontbindbaar is allemaal factoren van een lagere graad. De enige irreduciebele veeltermen in \mathbb{R}\left[x \right] zijn de eerste graads veeltermen en de tweedegraads veeltermen met een negatieve discriminant.
  • Een veelterm f(x) , verschillend van nul en van een eenheid, is een priem veelterm als voor alle veeltermen g(x) en h(x) geldt dat uit  f(x) | g(x).h(x) volgt dat f(x) | g(x) of f(x) | h(x). Voor reële veeltermen is priem veelterm een synoniem voor irreduciebele veelterm.
  • Elke van nul verschillende veelterm bezit een unieke ontbinding ( op toegevoegde elementen na).
  • Als 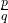\frac{p}{q} een rationaal nulpunt is van een veelterm met gehele coëfficiënten dan deelt p de coëfficiënt a_0 en q deelt a_n in \mathbb{Z}.

Veeltermfuncties

Geplaatst op door

De veelterm a_0+a_1x+a_2x^2+\cdots+a_nx^n met coëfficiënten in een getallenverzameling K, kan voorgesteld worden door de rij van de coëfficiënten (a_0,a_1,\cdots,a_n,0,0,\cdots) : een oneindige rij met een eindig aantal elementen verschillend van 0. Twee veeltermen zijn gelijk als de overeenkomstge rijen term gewijze gelijk zijn.

Met een veelterm kan je ook een veeltermfunctie associëren: f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n. Twee functies zijn gelijk als ze voor elk element van K hetzelfde beeld hebben.

Het is evident dat twee gelijke veeltermen gelijke veeltermfuncties bepalen, maar het omgekeerde niet; m.a.w. het is niet evident dat verschillende veelterm verschillende veeltermfuncties bepalen. Neem bvb. K=\mathbb{Z}_3=\{0,1,2\} ( we werken dus modulo 3). Nu zijn x en x^3 verschillende veeltermen want x=(0,1,0,0,...) en x^3=(0,0,0,1,0,0,...), terwijl de functies f(x)=x en g(x)=x^3 beide gelijk zijn aan \{(0,0),(1,1),(2,2)\}. Want 2^3=8 \equiv 2 \mod 3.

Voor K=\mathbb{R} kan men aantonen dat twee veeltermen gelijk zijn als en slechts als de overeenkomstige veeltermfuncties gelijk zijn.

Chebyshev veeltermen

Geplaatst op door

De Chebyshev-veeltermen T_n(x) zijn genoemd naar Pafnoeti Lvovitsj Chebyshev en zijn gedefinieerd door \cos nx uit  te drukken in functie van \cos x:

    \[T_n(x)=\cos(n\arccos x)\]

Zo is T_0(x)=1 en T_1(x)=x. Omdat \cos 2x=2\cos^2 x-1 is T_2(x)=2x^2-1. We weten ook dat \cos 3x = 4 \cos^3 x-3, dus is T_3(x)=4x^3-3x.

Dat T_n(x) een veelterm is van graad  n volgt uit de formule van Lemoivre. Andere Chebyshev veeltermen:

T_4(x)=8x^4-8x^2+1
T_5(x)=16x^5-20x^3+5x.

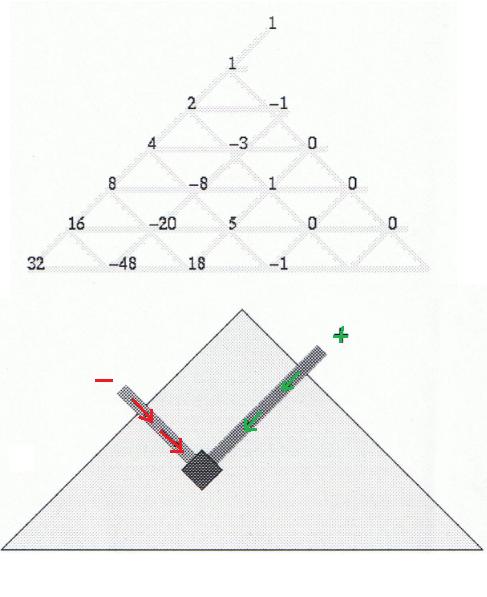
Het onderstaande driehoekig schema geeft een middel aan om de coëfficiënten te bepalen. Elk getal uit de driehoek bekom je door vanaf die positie alle getallen op de diagonaal naar rechtsboven bij elkaar op te tellenen hiervan dan alle getallen op de diagonaal naar linksboven af te trekken. Zo is bijvoorbeeld 18 = 5 + 1 + 0 – (-20) – 8.

 

 

grafieken T_n(x)

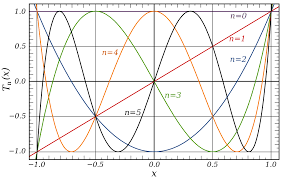
Je kan deze veeltermen ook krijgen via een recursie formule:

    \[T_{n+1}(x)=2xT_n(x)-T_{n-1}(x)\]

met T_0(x)=1 en T_1(x)=x.

Bovendien zijn de Chebyshev veeltermen ook oplossingen van volgende differentiaalvergelijking:

    \[(1-x^2)y''-xy'+n^2y=0\]