veelterm tweede greaad | Wiskunde is leuk

Zoek de maximale waarde van b in 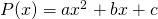$P(x)=ax^2+bx+c$ , als a,b en c reële getallen zijn en 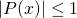$|P(x)|\leq 1$ voor $-1 \leq x\leq 1$ . Geef ook een veelterm die deze maximale waarde van b bereikt.

Antwoord

We weten dat $b=\dfrac{1}{2}(P(1)-P(-1))$ .
Nu zijn zowel $P(1)$ als $P(-1)$ volgens het gegeven kleiner dan of gelijk aan 1, dus is $b \leq \dfrac{1}{2}(1+1)=1$ .
De maximale waarde voor b is dus 1.
Neem $P(x)=\dfrac{1}{2}(x+1)^2-1$ . Omdat $0\leq x+1\leq 2$ is $|P(x) | \leq 1$ . Bovendien is na uitwerking $P(x)=\dfrac{1}{2}x^2+x-\dfrac{1}{2}$ , zodat $b=1$ .