Soms kan het probleem verdeeld worden in een aantal deelproblemen , die elk afzonderlijk kunnen behandeld worden. Dit gebeurt dikwijls als het probleem de al-kwantor bevat: voor alle x … Deze methode wordt ook wel het uitputtingsprincipe genoemd of de exhaustie methode.
Gegeven is een functie 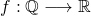 met
met
![]()
Bewijs dat ![]() .
.
- We gaan het resultaat eerst bewijzen voor de positieve gehele getallen. De eigenschap klopt voor x = 1.
Voor x = 2 hebben we .
.
Voor x = 3 is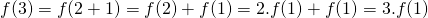 .
.
Het is duidelijk dat we dit proces kunnen verderzetten en dat voor elk positief geheel getal n geldt dat
- Nu controleren we de formule voor niet positieve gehelen. Eerst is er
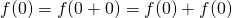 . Hieruit volgt dat
. Hieruit volgt dat  . Neem nu het negatief getal m, dan is er een positief geheel getal n met
. Neem nu het negatief getal m, dan is er een positief geheel getal n met 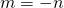 . Bijgevolg is
. Bijgevolg is  .
.
Hieruit volgt dat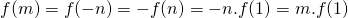 , waarmee het gestelde bewezen is.
, waarmee het gestelde bewezen is. - Nu komen de omgekeerden van de gehele getallen (verschillend van 0) aan de beurt. Stel
 , dan geldt:
, dan geldt:
 .
.
Hieruit volgt dat of
of 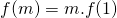 .
. - Tenslotte nemen we de rationale getallen onder de loep:
 .
.
Nu is .
.
Dus is .
.
Bijgevolg geldt voor elk rationaal getal dat
dat 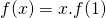 .
.


