Een stapel register kan eenvoudig voorgeteld worden als een systeem met een ingang(I) en een uitgang (U) met daartussen een wachtplaats( stapel of stack):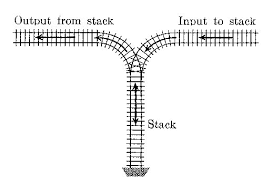
Neem de rij 123 en voer de volgende instructies uit: 3 in de stapel, 2 in de stapel, 2 uit de stapel, 1 in de stapel, 1 uit de stapel, 3 uit de stapel . De rij cijfers die aan de uitgang verschijnt is dan 213.
We zeggen dat 213 een stapelpermutatie is, omdat ze met een eindig aantal in en uit bewegingen kan bekomen worden van de oorspronkelijke rij 123. Van de zes ‘gewone’ permutaties van 123 is enkel 231 geen stapelpermutatie. Er zijn dus 5 stapelpermutaties van de rij 123.
Zijn er n elementen gegeven, dan is het aantal stapelpermutaties gegeven door
![]()
Dit getal noemen we het n-de Catalangetal. We spreken ook af dat ![]() . De eerste Catalaanse getallen zijn:
. De eerste Catalaanse getallen zijn: ![]() .
.
De naamgeving verwijst naar de Belgische wiskundige Eugene Catalan (Brugge 1814-Luik 1894). Catalaanse getallen vormen een fascinerende rij in de wiskunde, bekend om hun talrijke verschijningen in verschillende combinatorische problemen. Catalaanse getallen zijn een voorbeeld van hoe wiskundige structuren en patronen op onverwachte manieren kunnen opduiken. Een paar voorbeelden:
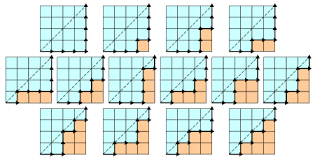
Een Dyck-pad van lengte 2n is een pad in een rooster dat niet onder de diagonaal komt en van naar loopt. Het aantal van dergelijke paden wordt gegeven door ![]() .
. 
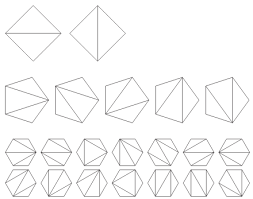
Het aantal manieren om een convexe -hoek op te splitsen in driehoeken met niet-overlappende diagonalen is gelijk aan ![]() .
.
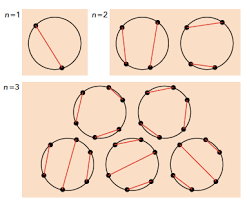
Het aantal manieren om 2n punten op een cirkelomtrek te verbinden met koorden die elkaar niet snijden is ![]() .
.