som termen rekenkundige rij | Wiskunde is leuk

Op hoeveel manier kan je, bijvoorbeeld, 45 schrijven als som van opeenvolgende getallen?

We stellen een formule op om de som van opeenvolgende getallen te berekenen. Stel $n=m+(m+1)+\dots+(m+k-1)$ . Hier bij is n de som, m het eerste getal en k het aantal getallen in die som.
Om die som te berekenen kan je de formule voor de som van de termen van een rekenkundige rij gebruiken: $n=\dfrac{1}{2}k.(m+m+k-1)$ .
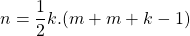Hieruit volgt:
$2n=k(2m+k-1)$
Als k even is dan is 2m + k – oneven en omgekeerd als k oneven is dan is 2m + k – 1 even. Bovendien is k kleiner dan 2m + k – 1.
We moeten 2n dus schrijven als een product van een even getal en een oneven getal. De kleinste van die 2 factoren is k en dat is het aantal termen in de som.
Ontbinden we n in priemfactoren: $n=2^r.p_1^{r_1}.\cdots .p_s^{r_s}$ . En dan is 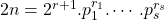$2n=2^{r+1}.p_1^{r_1}.\cdots . p_s^{r_s}$ . Hierbij zijn $p_i$ verschillende (oneven) priemgetallen. Dit moeten we dan schrijven als product van een oneven en even getal
Noteer S(n) het aantal mogelijkheden om n te schrijven als een som van opeenvolgende getallen, dan is het duidelijk dat
$S(n)=(r_1+1).\cdots.(r_s+1)-1$
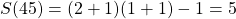Terug naar ons voorbeeld $n=45$ . dan is $2n=90=2.3^2.5^1$ en is $S(45)=(2+1)(1+1)-1=5$ . We kunnen 45 op 5 manieren schrijven als som van opeenvolgende getallen.
Hoe vinden we nu die sommen? We kunnen eerst m berekenen uit $2n=k(2m+k-1)$ : $m=\dfrac{1}{2}(n-k+1)$ en we nemen k opeenvolgend als 2,3,5,6,9. Dit geeft:
$\begin{array}{c|c|c} k&m&\text{som}\\ \hline 2&22&22+23\\3&14&14+15+16\\5&7&7+8+9+10+11\\6&5&5+6+7+8+9+10\\9&1&1+2+3+4+5+6+7+8+9\end{array}$

Wiskunde is leuk