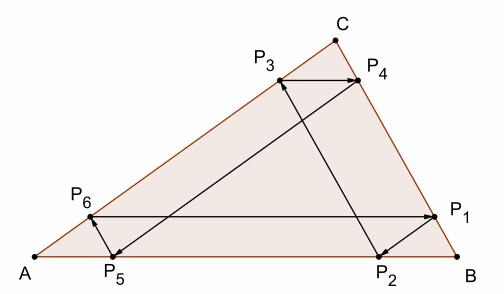
Neem een punt 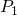op de zijde [BC] van een driehoek ABC. Trek een evenwijdige met AC en noem het snijpunt met [AB] het punt 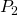. Trek van daaruit een evenwijdige met BC en noem het snijpunt met [AC`] het punt 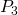. Als je zo verder gaat komt je uiteindelijk terug in het punt 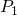. Dit resultaat staat bekend als de sluitingsstelling van Thomsen.

Kies een doorloop zin voor de driehoek zodat een punt de zijde verdeelt in een ‘eerste ‘ en een ’tweede ‘ deel. verdeelt [BC] in twee stukken met verhouding . Door de evenwijdigheid zal dan de zijde [AB] verdelen in 2 stukken met verhouding

De verhouding keert dus om telkens we een andere zijde bereiken. Bij elke  3 stappen zitten we terug op het lijnstuk [BC].. Na 6 stappen komen we dus terug op [BC] en nu is de verhouding van de stukken dezelfde als in het begin. Dus zal samenvallen met .

Dit resultaat danken we aan Gerhard Thomsen , een Duitse wiskundige die leefde van 23/6/1899 tot 4/1/1934.