Tag archieven: Schwarz

Ongelijkheid van Cauchy-Schwarz

Geplaatst op door

Stel (a_1,a_2,\cdots,a_n) en (b_1,b_2,\cdots,b_n)  n-tallen van reële getallen, dan geldt:

(a_1b_1+a_2b_2+\cdots+a_nb_n)^2\leq(a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2)

Deze ongelijkheid werd genoemd naar A.L.Cauchy( 1789-1857) en H.A.Schwarz(1843-1921) en steunt op de eigenschap dat het skalair product van twee vectoren kleiner is dan of gelijk is aan het product van de normen van die vectoren.


 

 

 

 

 

 

Bekijken we even een voorbeeld:

Bewijs: 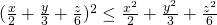(\frac{x}{2}+\frac{y}{3}+\frac{z}{6})^2 \leq \frac{x^2}{2}+\frac{y^2}{3}+\frac{z^2}{6}

Het is enkel de kwestie van goed de twee drietallen te kiezen.
Neem (\frac{x}{2},\frac{y}{\sqrt{6}},\frac{z}{\sqrt{12}}) en  (1,\sqrt{\frac{2}{3}},\sqrt{\frac{2}{6}}) en vul in.