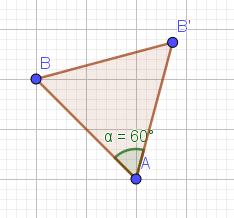
Gegeven zijn 2 punten A en B. Als we B roteren  over 60° rond A, naar het punt B’, dan is de driehoek ABB’ gelijkzijdig.

Een gevolg hiervan is de volgende eigenschap over gelijkzijdige driehoeken die gevonden werd in 1936 door de Roemeense wiskundige D.Pompeiu (1873-1954). Het is merkwaardig dat dit, relatief eenvoudig resultaat, niet vroeger ontdekt werd.

ABC is een gelijkzijdige driehoek en P een punt dat niet op de omgeschreven cirkel ligt van ABC. Dan is het steeds mogelijk een driehoek te construeren met als zijden PA,PB en PC. Als P toch op de omgeschreven cirkel ligt dan zal een van deze drie lengtes gelijk zijn aan de som van de anderen.

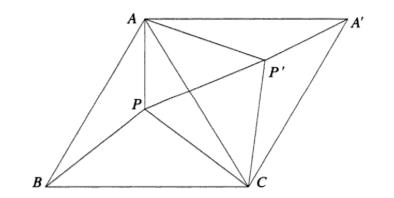
In onderstaande tekening wordt ABC over 60° gedraaid rond het punt C. De zijden van de driehoek PP’A zijn gelijk aan PA,PB en PC, dus hebben we inderdaad een driehoek geconstrueerd met als zijden PA,PB en PC.