Tag archieven: recursievergelijking

Marginale kosten

Geplaatst op door

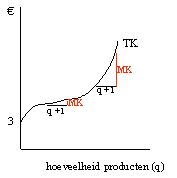
De marginale kostprijs, dit is de kostprijs om de productie van n stuks per dag op te voeren met 1 eenheid, wordt gegeven door

    \[M(n)=10000-2n+0,004n^2\]

Bereken de meerkost,  genoteerd met M(n,m),  om de productie op te voeren van 400 naar 450 stuks.

Noteer met K(n) de totale kostprijs voor de productie van n stuks per dag. De marginale kostprijs op niveau n is dan

    \[M(n)=K(n+1)-K(n)\]

We weten dus dat K(n+1--K(n)= 10000-2n+0,004n^2. Dit is een recursievergelijking. Eigenlijk is dit de discrete tegenhanger van het begrip afgeleide. Het is dus niet onredelijk te veronderstellen dat K(n) een derdegraadsveelterm is. Noteer K(n)=a+bn+cn^2+dn^3. Invullen is de recursievergelijking geeft de oplossingen voor a,b,c en d. We vinden b = 10001,00067; c = -1,001 en c = 0,0013333.

Dan is M(400,450) = 493632.