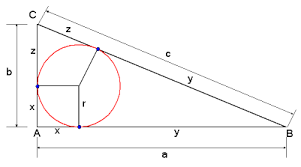
Zoek een verband tussen de zijden van een rechthoekige driehoek en de straal van de ingeschreven cirkel.
De stukken van de raaklijnen vanuit een punt aan de cirkel zijn even lang en bovendien is x = r.
Wanneer we 
berekenen vinden we dat 
, dus geldt in een rechthoekige driehoek :
![\[a+b-c=2r\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-27432c82a9f4a974443e744c956ee9ef_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
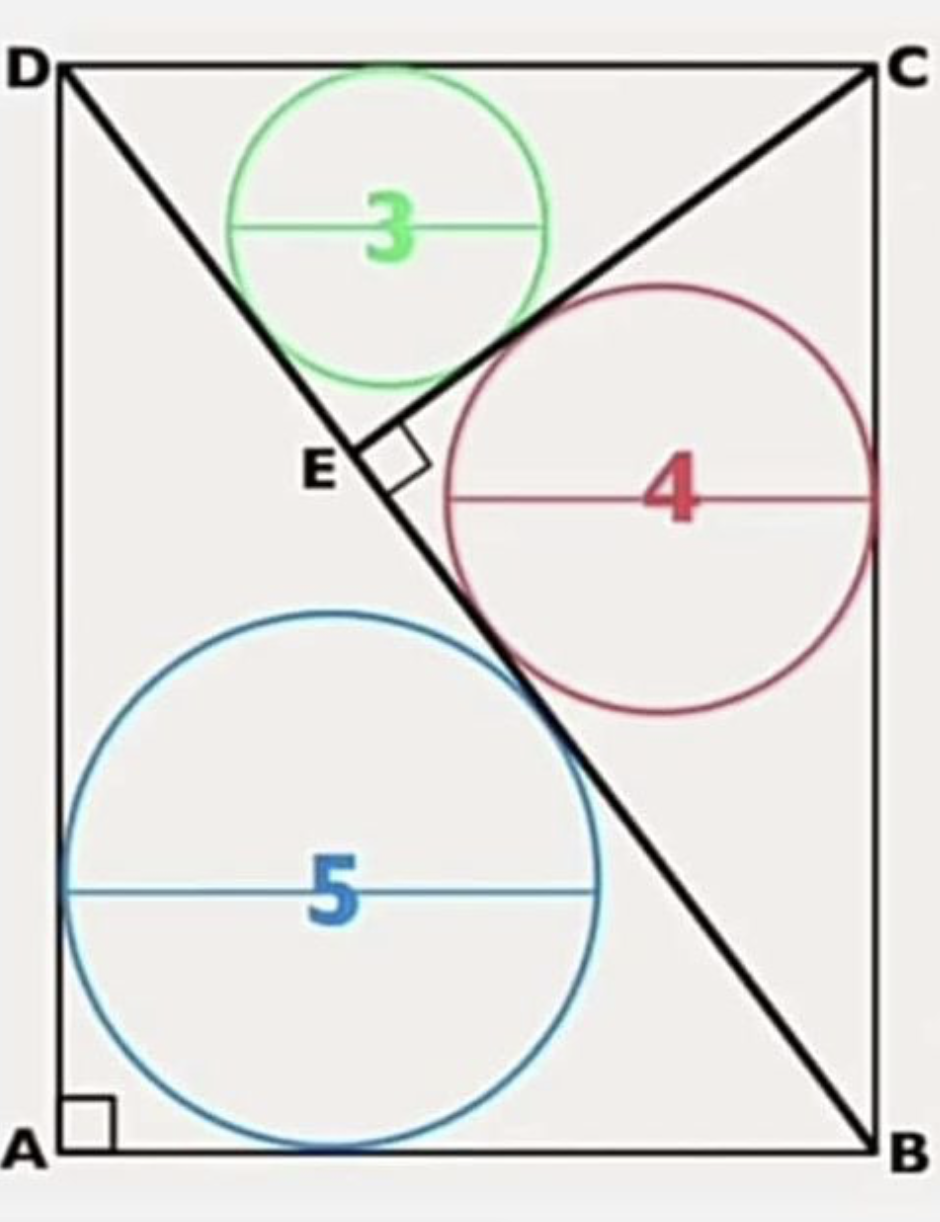
Kan je nu de oppervlakte van de rechthoek ABCD berekenen?
en als hoogte 
. De gevraagde oppervlakte bedraagt dus 3 oppervlakte eenheden.
.
.
.
, met c de schuine zijde. Maar de zwaartelijn getrokken naar de schuine zijde is gelijk aan de helft van die schuine zijde. Dus 
.
gelijk aan het dubbele van de oppervlakte van de driehoek, dus 
.
.
.![\[A=\frac{x^2+x\sqrt{x^2+8y^2}}{4}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-62ed6e76d59f6b71e4981024e29c7492_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
en 
. Hierbij zijn u en v onderling ondeelbaar en is één ervan even en de ander oneven. Bovendien is d de grootste gemene deler van de drie zijden en 
.
of uitgedrukt in u en v : 
.
zeker oneven is en een deler is van 4 moet 
. Ook moet 
of 4. Hieruit volgt dat 
of 5 en 
of 1.
en 
.