Er bestaat een mooie, minder bekende meetkundige stelling, die voor het eerst gevonden werd door de Schotse wiskundige William Wallace (1768-1843).
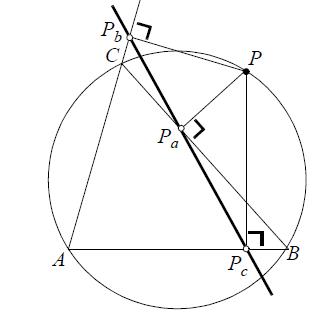
De voetpunten Pc , Pa en Pb van de loodlijnen uit een punt
P van de omgeschreven cirkel van driehoek ABC neergelaten
op de dragers van de zijden, zijn collineair.
De rechte door Pa,Pb en Pc noemt men de rechte van Wallace.
Het bewijs verloopt als volgt: PBPcPa is een koordenvierhoek (hoek tussen zijde en diagonaal). Analoog zijn ook PPaCPb en PCAB koordenvierhoeken. Omdat de overstaande hoeken supplementair zijn volgt hieruit dat 
. Hieruit volgt dat de drie punten collineair zijn.
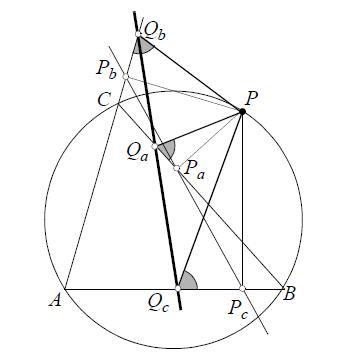
Men kan deze stelling ook veralgemenen:
Als je in plaats van loodlijnen, rechten uit P kiest die eenzelfde hoek maken met de zijden, dan geldt weer dat de drie ‘voetpunten’, zeg Qc, Qa en Qb, collineair zijn.
