In elke groep van 6 personen zijn er altijd 3 die elkaar kennen of 3
die elkaar niet kennen.

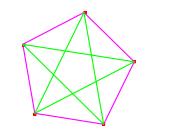
Dit is niet noodzakelijk waar in een groep van 5
personen.

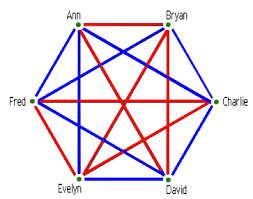
Het probleem is ook gekend met 6 punten waarbij alle verbindingslijnstukken ofwel in het rood ofwel in het blauw gekleurd worden. Bewijs dat minstens één  driehoek kan gevonden worden die drie gelijkgekleurde zijden heeft. We hebben hier te maken met een volledige graaf waarvan de zijden in twee mogelijke kleuren worden ingekleurd.

Wij gaan het probleem aanpakken in een iets moeilijker versie:

Gegeven 17 punten: die willekeurig in
het vlak  liggen. Men trekt tussen deze punten alle verbindingslijnstukken, hetzij rood, hetzij blauw, hetzij groen. Bewijs dat minstens één  driehoek kan gevonden worden die drie gelijkgekleurde zijden heeft.

• Kies een willekeurig punt uit het zeventiental en beschouw de zestien verbindingslijnstukken die dat punt met de zestien andere punten verbindt.
• Volgens het duivenhokprincipe is het steeds mogelijk uit die zestiental lijnstukken een zestal te vinden die dezelfde kleur hebben. Laten we aannemen dat de zes gekozen lijnstukken allemaal rood
  zijn.
• De zes rode lijnstukken verbinden het eerstgekozen punt met een zestal andere punten. We richten nu onze aandacht op dat zestal en in het bijzonder op hun verbindingslijnstukken.
• Vinden we bij die verbindingslijnstukken een rood exemplaar, dan vormt dit met de beide rode liinstukken  een rode driehoek en dan zijn we klaar.
• Het ergste, wat ons overkomen kan, is  dat die zes punten alleen groene en blauwe verbindingslijnstukken hebben. Laten we dus aannemen, dat dit het geval is.
• Kies uit het zestal punten nu een willekeurig punt uit en beschouw de vijf verbindingslijnstukken van dit punt met de vijf andere punten van het zestal.  Kies er drie uit die dezelfde kleur hebben .Dat dit mogelijk is volgt weerom uit het duivenhokprincipe.
• Laten we aannemen, dat ze alle drie groen zijn. Tenslotte letten we op de verbindingslijnstukken van die drie andere punten. Deze
  zijn groen of blauw. Is er een van die verbindingslijnstukken groen, hebben we een groene driehoek gevonden. En er is geen groene bij, dan vormen ze zelf een blauwe driehoek.

We kunnen dit veralgemenen voor kleuren . Noteer met het aantal punten dat er nodig is om met kleuren steeds een driehoek te vinden met gelijkgekleurde zijden. Dan geldt: