Tag archieven: rakende cirkels

Sangaku 3

Geplaatst op door

Antwoord

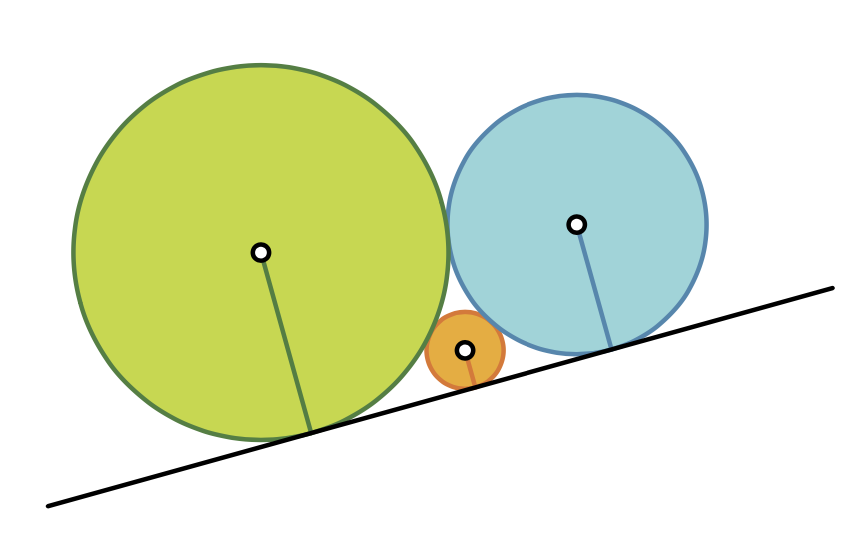
  • We zien hier 3 cirkels die elkaar uitwendig raken en die alle 3 eenzelfde rechte raken. We zoeken een verband tussen de stralen. Noem die, van links naar rechts, r_1,r_2 en r_3.
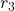  • Bij twee dergelijke cirkels zien we dat

        \[|xy|^2=(r+s)^2-(r-s)^2=4rs\]

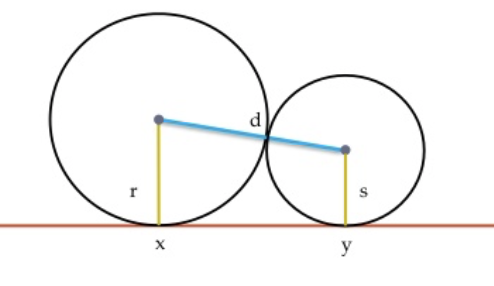
  • We kunnen dit 3 keer toepassen in de gegeven sangaku: de twee linkse cirkels, de twee rechtse cirkels en de meest linkse met de meest rechtse. Zo vinden we \sqrt{r_1r_3}=\sqrt{r_1r_2}+\sqrt{r_2r_3}
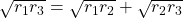
  • Na deling van beide leden door \sqrt{r_1r_2r_3}, vinden we:

        \[\frac{1}{\sqrt{r_2}}=\frac{1}{\sqrt{r_1}}+\frac{1}{\sqrt{r_3}}\]

 

Inversie

Geplaatst op door

We kennen de spiegeling rond een rechte als transformatie van het vlak. De dekpunten zijn de punten van de” rechte en lengte en hoeken zijn invarianten. Maar er betaat ook een spiegeling in een cirkel: de inversie. Lees in bijgevoegde tekst  hoe dit tewerk gaat en hoe je die techniek kan gebruiken om bepaalde meetkundige problemen over o.a. orthogonale cirkels en rakende cirkels, eenvoudiger op te lossen.

Het begrip inversie hebben we te danken aan de Zwitserse wsikundieg Jacob Steiner ( 1796-1863). Het wiskundige werk van Steiner beperkte zich tot meetkunde. Hij behandelde dit synthetisch en geheel niet analytisch.

 

Kussende cirkels

Geplaatst op door

In de meetkunde is de stelling van Descartes, vernoemd naar René Descartes, een relatie tussen de stralen van vier onderling rakende cirkels.

De stelling geeft aan hoe uitgaande van drie onderling rakende cirkels een vierde cirkel te construeren is die aan deze drie raakt.In dit artikel gaan we het hebben over dergelijke problemen.