Tag archieven: python

Een probleem uit getallenleer

Geplaatst op door

Een natuurlijk getal bestaat uit 9 verschillende cijfers 1 tot en met 9. Schrijft men het opnieuw met telkens de eerste k cijfers, dan is het getal een veelvoud van k. Om welk getal gaat het?

 

  • Het getal gevormd door de eerste 2 cijfers is dus deelbaar door 2, gevormd door de eerste 3 cijfers door 3,…Het getal zelf is dus deelbaar door 9.
  • Dat laatste is altijd voldaan omdat de som der cijfers gelijk is aan 45 en dat is deelbaar door 9. Bijgevolg is het getal zelf ook deelbaar door 9. 
  • We moeten dus enkel controleren voor de eerste 2 tot de eerste 8 cijfers.
  • Het volgende programma in Python geeft de oplossing:

Python: de zeef van Eratosthenes

Geplaatst op door

De zeef van Eratosthenes  (Bibliothecaris van de bibliotheek van Alexandrië rond 240 v.C.) is een algoritme om priemgetallen te bepalen kleiner dan een gegeven getal n:

  • Maak een geordende lijst van alle getallen van 2 tot n.
  • Neem het kleinste getal in deze lijst en schrap alle veelvouden van dit getal ( het getal zelf niet!).
  • Neem het volgende getal in de lijst en doe hiervoor hetzelfde.

Een programma in Python geeft bijvoorbeeld alle priemgetallen kleiner dan 50

:

Uitleg: 

  • Neem een lijst van lengte n en zet op elke plaats de boolse waarde True.
  • Begin met p=2 en zet alle veelvouden van 2 in de lijst op False. Begin met het eerste veelvoud van 2 na 2 zelf: dat is 2*2.
  • Neem dan p=3 en zet alle veelvouden van 3 op False, beginnend met 3*3 
    (want alle vroegere veelvouden zijn sowieso al op False gezet.
  • Doe zo verder zolang p*p kleiner is dan de gegeven waarde n.

Priemtweelingen

Geplaatst op door

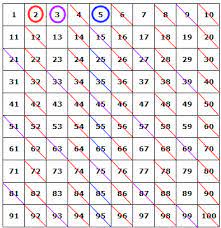
Een paar opeenvolgende priemgetallen waarvan de afstand 2 is, noemen we een priemtweelingen. Buiten de eerste priemtweelingen 3-5 vinden we bijvoorbeeld ook 5-7, 11-13, 17-19,… Ze ontstaan allemaal (behalve 3-5), door vertrekkend van 5-7, een translatie uit te voeren over 6 eenheden. Dit is logisch want een priemgetal is altijd van de vorm 6k+1 of 6k-1. 

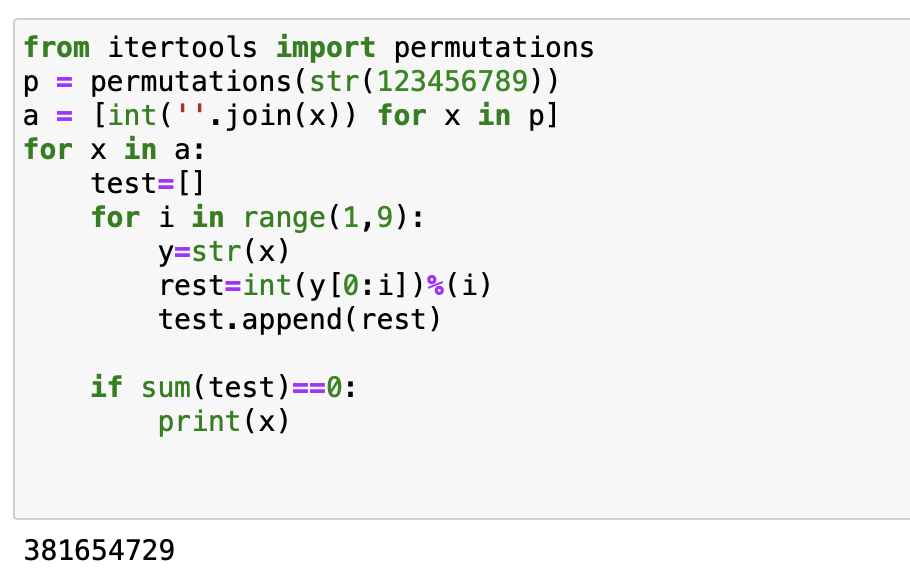
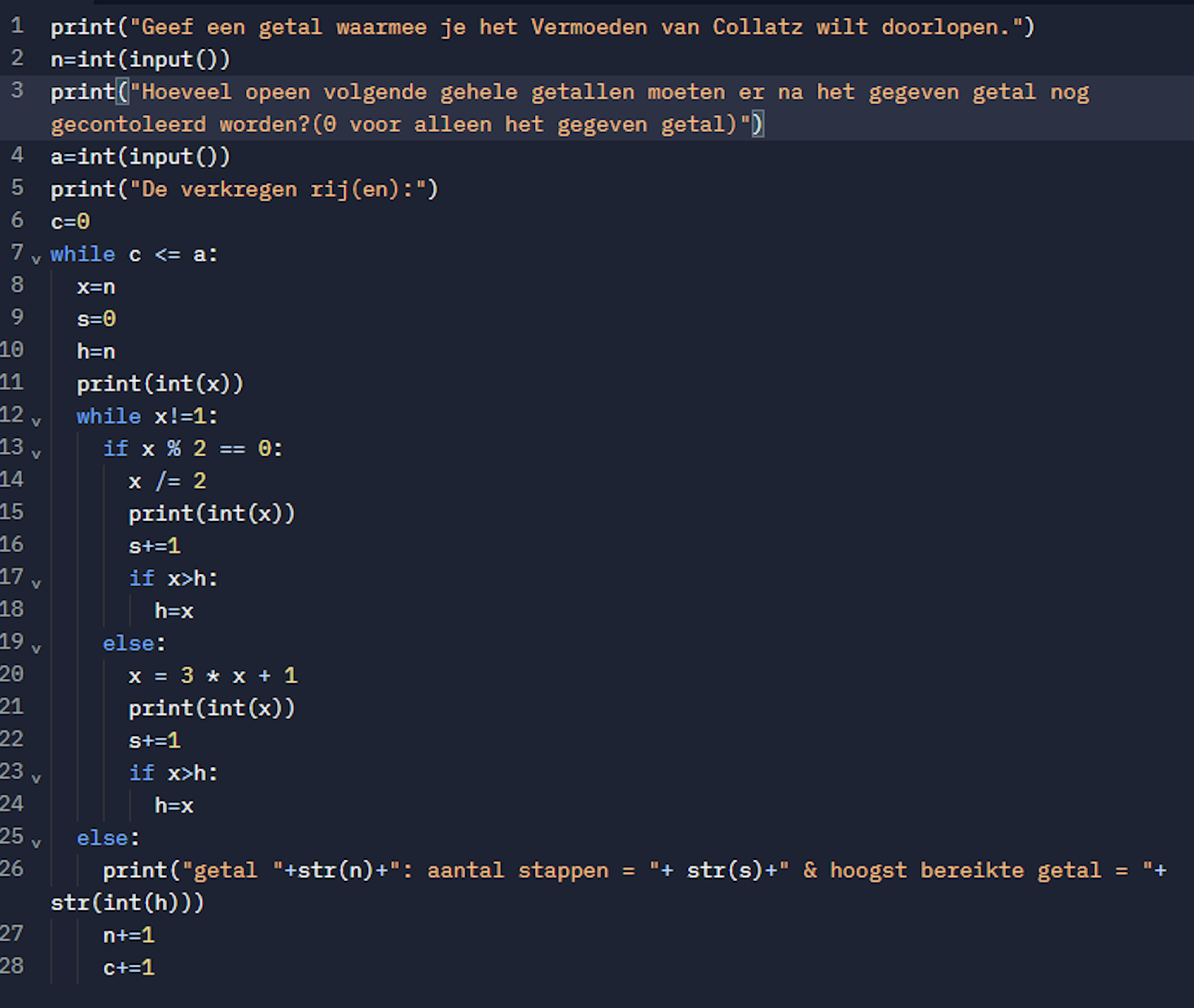
Een Python programma om alle priemtweelingen kleiner dan 1000 te bepalen:
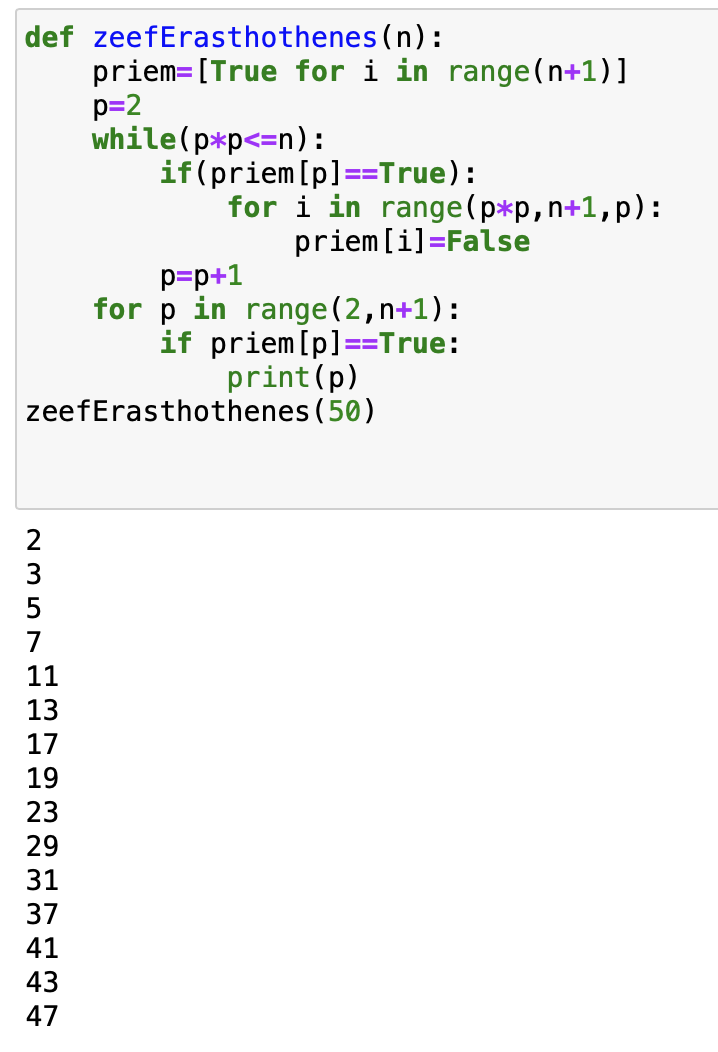
De output:

Een paar ‘leuke ‘ eigenschappen, die zeer eenvoudig te bewijzen zijn:

  • Een priemtweelingen heeft een symmetriemidden dat steeds een 6-voud is.
  • De som van twee elementen van een priemtweelingen is steeds een 12-voud.
  • De afstand voor de overeenkomstige elementen van twee priemtweelingen is steeds een 6-voud.
  • De afstand van het grootste getal van de kleinste priemtweeling tot het kleinste getal van de grootste priemtweelingen is een 6-voud min 1.
  • Er bestaat geen grootste priemtweeling.