Wiskunde is leuk

Nootje 37

Geplaatst op 11 juni 2023 door admin

Antwoord

Vermoedelijk een toepassing op de stelling van Pythagoras….
Men kan gemakkelijk bewijzen dat
$|PD|^2+|PB|^2=|PA|^2+|PC|^2$
Dit resultaat wordt weleens de stelling van de Britse vlag genoemd, naar de vergelijking met de Union Jack
Voor ons probleem is dus $x^2+4=36+49$ , dus is $x=9$ .

Sangaku 11

Geplaatst op 29 december 2022 door admin

Antwoord

De bedoeling is de oppervlakte van het vierkant te bepalen.
De horizontale rechthoekzijde van de rode driehoek is gelijk aan $\sqrt{27}-\sqrt{12}=\sqrt{3}$ . De andere rechthoekszijde meet $\sqrt{12}=2\sqrt{3}$ en is dus dubbel zo groot als de horizontale rechthoekzijde.
De zwarte driehoek is gelijkvormig met de rode en omdat de verticale rechthoekzijde gelijk is aan $\sqrt{3}+\sqrt{12}+\sqrt{27}=6\sqrt{3}$ , moet de horizontale rechthoekzijde gelijk zijn aan de helft ervan , dus $3\sqrt{3}$ .
Volgens de stelling van Pythagoras is het kwadraat van de zijde van het vierkant dan gelijk aan $(6\sqrt{3})^2+(3\sqrt{3})^2=135$
De gevraagde oppervlakte is dus 135.

Nootje 30

Geplaatst op 4 november 2022 door admin

Bereken $|AB|$ :

“Antwoord”

Construeer vanuit het middelpunt van de kleine cirkel een loodlijn op de straal uit A in de grote cirkel. AB staat , als gemeenschappelijke raaklijn aan de twee cirkels, loodrecht op de stralen in A en B.
Uit de stelling van Pythagoras volgt dan: $|AB|=x=\sqrt{(28+18)^2-10^2}=12\sqrt{14}$ .

Sangaku 9

Geplaatst op 17 juli 2022 door admin

Spoiler

We zoeken de verhouding tussen de rode en blauwe oppervlakte.

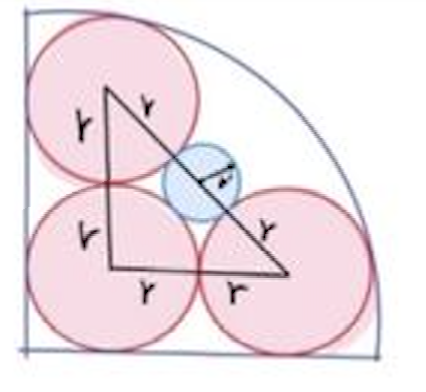Noem de straal van de rode cirkels r en die van de blauwe cirkel r’.
De schuine zijde van de getekende rechthoekige driehoek kan je berekenen via de stelling van Pythagoras: $\sqrt{(2r)^2+(2r)^2}=2\sqrt{2}r$ .
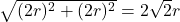Maar dan is 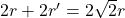$2r+2r'=2\sqrt{2}r$ . Of $r'=r(\sqrt{2}-1)$ .
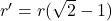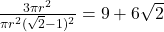De gezochte verhouding is dan $\frac{3\pi r^2}{\pi r^2(\sqrt{2}-1)^2}=9+6\sqrt{2}$ .

Sangaku 8

Geplaatst op 11 februari 2022 door admin

Antwoord

De opdracht kan zijn de straal te berekenen van de kleine cirkels.
Noem r de straal van een kleine cirkel
Gebruik van Pythagoras geeft : r=1 of $r=\frac{1}{9}$
r = 1 kan natuurlijk niet, dus de straal van de kleine cirkel is $r=\frac{1}{9}$