Tag archieven: Pythagoras

Wortelspiraal

Geplaatst op door

De term “wortel spiraal” verwijst naar de spiraal van Theodorus, een meetkundige constructie om de vierkantswortels van opeenvolgende natuurlijke getallen te visualiseren.  De spiraal bestaat uit een reeks aaneengeschakelde rechthoekige driehoeken, waarbij elke driehoek aan de vorige wordt geplaatst. De schuine zijde van de volgende driehoek is de wortel van het volgende natuurlijke getal, en de lengte daarvan wordt bepaald door de stelling van Pythagoras. 

Nootje 58

Geplaatst op door

In een rechthoekige driehoek met zijden 3,4 en 5 teken je de ingeschreven cirkel en een cirkel die daaraan raakt en ook raakt aan twee zijden van de driehoek, zoals in onderstaande tekening. Bepaal de straal van de kleinste cirkel.

Antwoord

  • Noem R de straal van de ingeschreven cirkel,  dan moet 3-R+4-R=5, omdat raaklijnen getrokken aan een cirkel uit een bepaald punt, even lang zijn. Dus is R=1.
  • Noem r de straal van de kleine cirkel.
  • De aangegeven afstand vind je ofwel via de stelling van Pythagoras ofwel via de gelijkvormigheid van driehoeken.
  • Dan is 1+r+\sqrt{10}r=\sqrt{10}, waaruit volgt dat

        \[r=\frac{\sqrt{10}-1}{\sqrt{10}+1}\]

 

De spiraal van Theodorus

Geplaatst op door

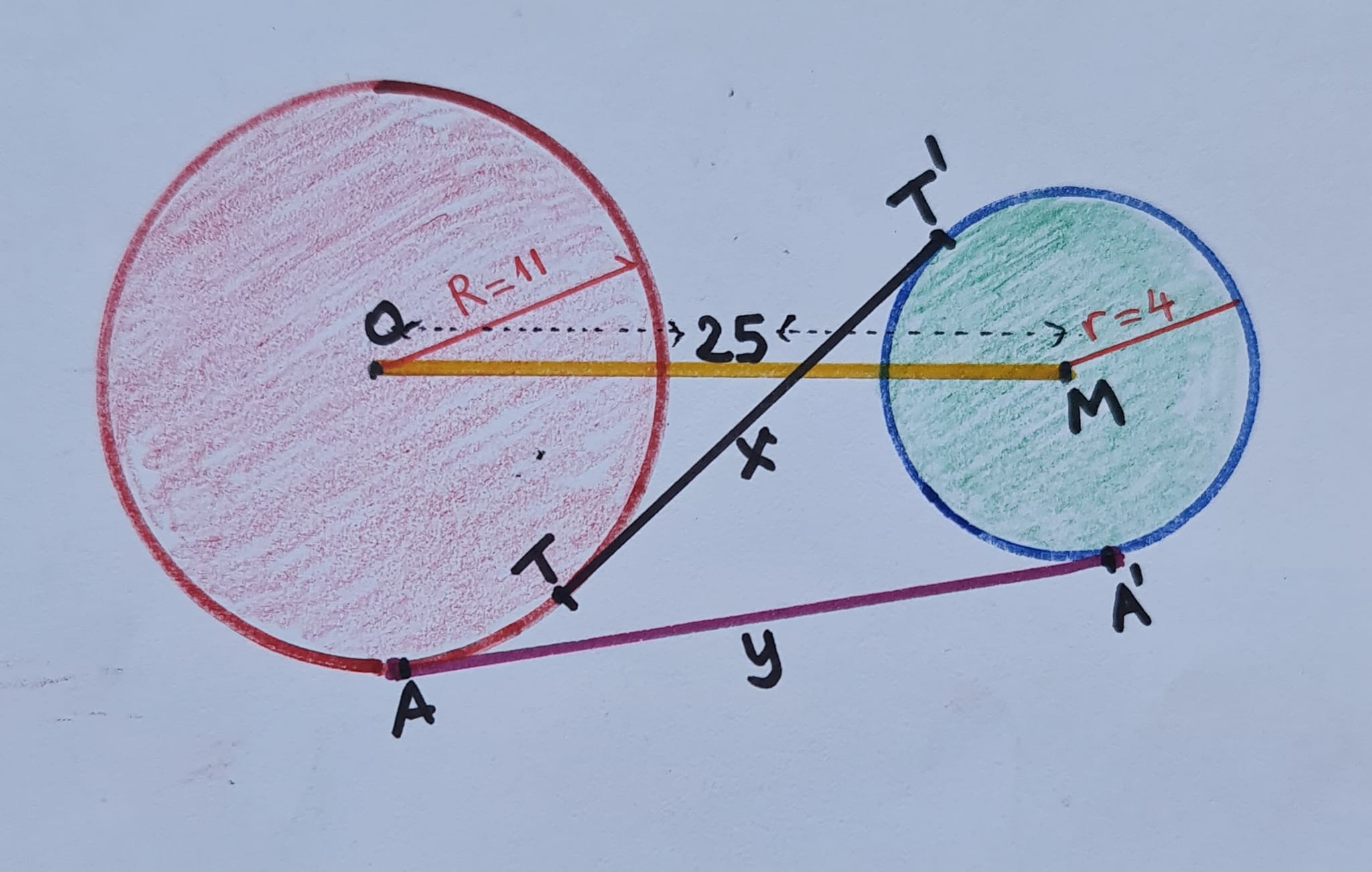
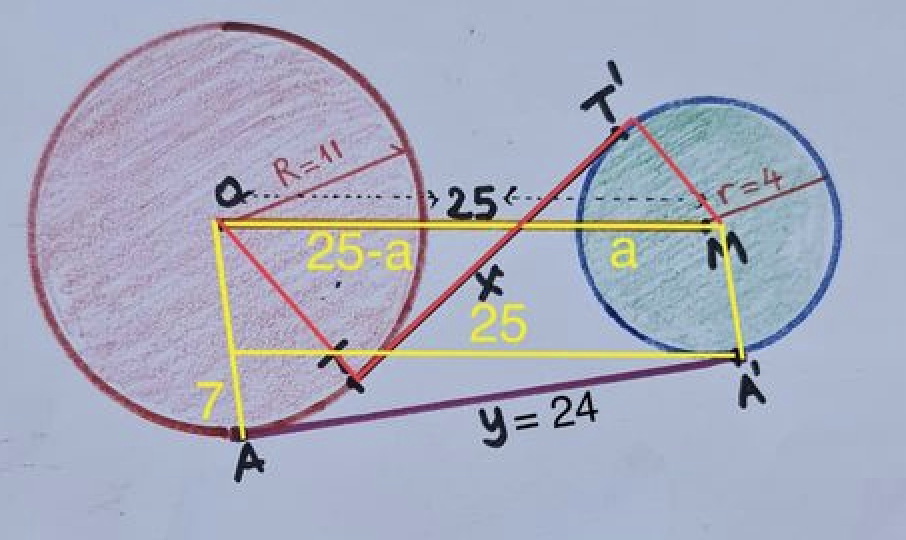
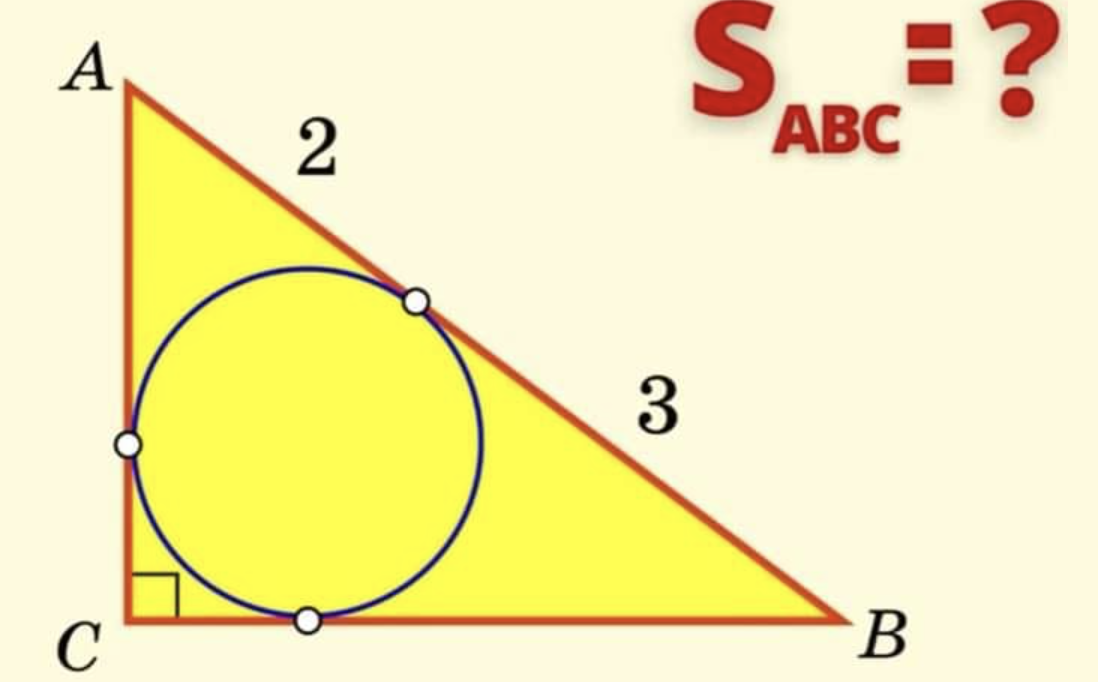
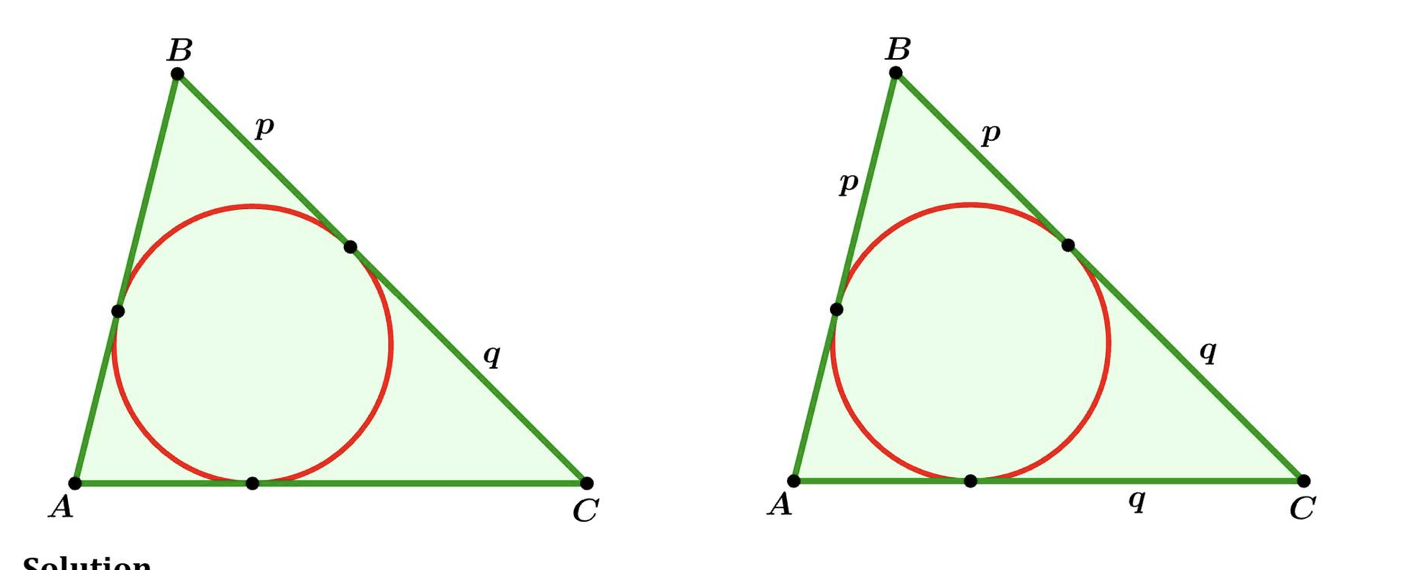
De spiraal van Theodorus wordt opgebouwd uit een reeks rechthoekige driehoeken. Het begint met een gelijkbenige rechthoekige driehoek waarvan de beide rechthoekszijden lengte 1 hebben. Vervolgens wordt een nieuwe rechthoekige driehoek toegevoegd, waarbij één rechthoekszijde de vorige schuine zijde is en de andere rechthoekszijde terug lengte 1 heeft. Dit proces wordt herhaald. De figuur die zo ontstaat noemt men de spiraal van Theodorus, genoemd naar de Griekse wiskundige Theodorus van Cyrene die leefde in de 5de eeuw voor Christus.

Hij hield op bij de driehoek met hypotenusa \sqrt{17} , vermoedelijk omdat dat de laatste is die niet een vorige driehoek overlapt.

Het is duidelijk dat via de stellig van Pythagoras  de lengten van de  schuine zijden van deze driehoeken de vierkantswortels zijn van opeenvolgende natuurlijke getallen. Vandaar dat men deze spiraal ook wel eens wortelspiraal noemt.