Tag archieven: puzzel

Magische driehoek

Geplaatst op door

Plaats de cijfers van 1 tot en met 9 in de cirkeltjes in het diagram zodat de som van de vier cijfers langs de drie zijden gelijk is aan 17. En hoe kan je ze rangschikken zodat de som langs de drie zijden telkens gelijk is aan 20? Is er een andere som mogelijk? 

Deze puzzel komt uit het boek The Moscow puzzels van Boris Kordemsky(1907-1999), een wiskundedocent uit Moskou.

Spoiler

De drie snelste paarden

Geplaatst op door

De eigenaar van een mooie renstal met 25 paarden wil uitzoeken welke drie paarden het snelst zijn. Hij kan dit echter alleen doen door de paarden tegen elkaar te laten lopen. Maar hij kan slechts vijf paarden tegelijkertijd  laten lopen. Hoeveel races heb je minimaal nodig om de drie snelste paarden te selecteren. 

  • Verdeel de 25 paarden in 5 groepjes van 5 en duid in elke groep het snelste paard aan door 5 races te organiseren. Laat in de zesde wedstrijd de 5 winnaars tegen elkaar uitkomen. Zo kan het allersnelste paard worden aangeduid in 6 races.
  • Om het tweede en derde snelste paard aan te duiden heb je maar 1 extra wedstrijd nodig: 

    In de tekening hierboven staan de paarden per groep, van links naar rechts, in volgorde van snelheid. de traagste helemaal links. De groepen zelf zijn gerangschikt van onder naar boven volgens de snelheid van hun winnaar; de traagste helemaal onderaan. In het rood zijn alle paarden aangeduid waarvan we weten dat er nog minstens drie snellere paarden zijn. Er blijven nog zes paarden over. Het paard rechtsboven is de allersnelste en laten we even buiten beschouwing. Laat de vijf andere tegen elkaar lopen in de zevende race.  Zo vinden we de zilveren en bronzen medaille!

 

Even huisnummers

Geplaatst op door

Ik woon aan de kant van de even huisnummers in mijn straat. Als ik de huisnummers van de huizen links van mij optel en daarna die van rechts, dan zijn die twee sommen gelijk. Hoeveel huizen staan er aan de even kant in mijn straat en op welk nummer woon ik?

Veronderstel dat ik in het (k+1) ste huis woon, dan staan er k huizen links van mij, met nummers 2,4,6,…,2k. Dit zijn termen van een rekenkundige rij en dus kunnen we de som berekenen:

    \[S_l=\frac{1}{2}k.(2+2k)=k^2+k\]

Als er n huizen staan in mijn straat, dan bevinden zich rechts van mij nog n-k-1 huizen, met nummer 2k+4,2k+6,…,2n. Ook hier hebben we een rekenkundige rij, dus :

    \[S_r=\dfrac{1}{2}(n-k-1)(2k+4+2n)=(n-k-1)(n+k+2)\]

Nu moet S_l=S_r. Dit geeft na uitwerking:

    \[2k^2+4k-(n^2+n-2)=0\]

Dit is een Diophantische vergelijking. We zoeken naar gehele oplossingen . Bijgevolg moet k=\dfrac{-4 \pm \sqrt{16+8(n^2+n-2)}}{4} \in \mathbb{Z}. Hieruit volgt:

    \[k=-1 \pm \sqrt{\frac{1}{2}(n^2+n)} \in \mathbb{Z}\]

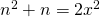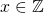Daarom moet n^2+n =2x^2 met x\in \mathbb{Z}. Dit valt te herschrijven als

    \[(2n+1)^2-8x^2=1\]

Vergelijkingen van de vorm 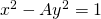x^2-Ay^2=1 noemt men vergelijking van Pell. Dit type vergelijkingen is moeilijk op te lossen, maar we kunnen wel een aantal oplossingen ‘proberen’, omdat de straten bij ons niet zo lang zijn.  Zo vinden we :

    \[\begin{array}{c|c|c} n&k+1&\text{huisnummer}\\ \hline \\ 1&1&2\\8&6&12\\49&35&70\\288&204&408 \end{array}\]

De eerste  oplossing is een beetje absurd: een straat met maar 1 huis. Bij de tweede oplossing telt de straat 8 huizen langs de even kant en woon ik in huisnummer 16. Links van mij heb je de nummers 2,4,6,8 en 10 met som 30 en rechts van mij de nummers 14 en 16, ook met som 30. De derde oplossing geeft een straat met 49 huizen en ik woon op nummer 70.