Een programma in Python om de god en het ktv van twee getallen te berekenen. We maken gebruik van het algoritme van Euclides, dat zegt dat de grootste gemene deler van a en b ( met a>b) gelijk is aan de grootste gemene deler van b en de rest bij deling van a door b. Verder gebruiken we de formule dat het product van de ggd en het kgv gelijk is aan het product van de twee gegeven getallen.
een voorbeeld:
Schrijf in Python een programma dat zelf een getal kiest tussen 1 en 100. Jij moet raden welk getal het is. de computer geeft enkel aan of je lager of hoger moet gokken.
Een paar opmerkingen:
Een mogelijke output :
Python bezit de mogelijkheid zelf functies te definiëren. Zo kunnen we bijvoorbeeld de kwadraatfunctie definitiëren:
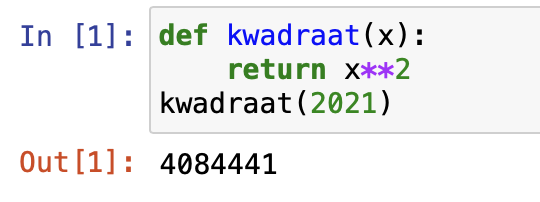Het begin van een functie duiden we aan met def , nadien komt de naam en tussen de haakjes staan de argumenten, in dit geval dus gewoon x. Na return komt er wat de functie moet teruggeven. het is ook mogelijk om: meerdere argumenten te geven. Als je in een programma vaak iets moet berekenen, maak je best een functie voor die berekening.
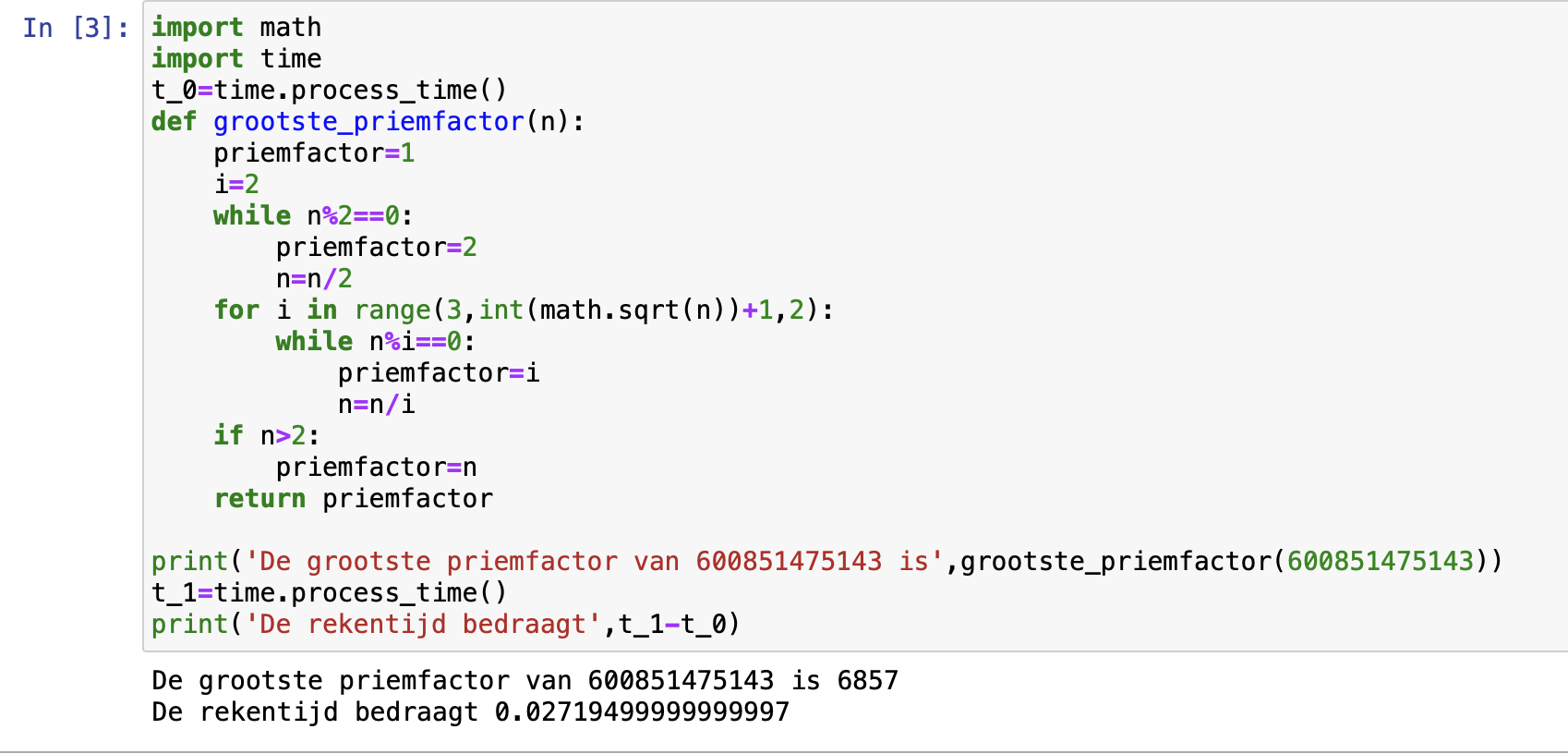
Je kan in Python zelfs gebruik maken van de functie in de functie zelf! We kunnen bijvoorbeeld gebruik maken van de recursieve relatie van faculteiten om hiervoor een functie te maken:
De functie zal zichzelf aanspreken.Je hebt natuurlijk ook beginwaarden nodig, anders kan je nooit een antwoord geven voor een willekeurige n. Als, zoals in ons voorbeeld, n = 20 zal de functie na 19 keer zichzelf aan te spreken, een 1 teruggeven, en dus eindigen.
Als de herhalingen eerder afhangen van een bepaalde voorwaarde, kan je beter een while-lus gebruiken.
Alle iteraties zullen uitgevoerd worden, zolang de voorwaarde
achter de while geldt. In bovenstaand voorbeeld zal zolang i < 6, de waarde van i afgedrukt worden, en zal telkens met 1 worden vermeerderd.