Tag archieven: problem solving

Bericht navigatie

Geplaatst op 11 juni 2023 door admin

Antwoord

Vermoedelijk een toepassing op de stelling van Pythagoras….
Men kan gemakkelijk bewijzen dat
$|PD|^2+|PB|^2=|PA|^2+|PC|^2$
Dit resultaat wordt weleens de stelling van de Britse vlag genoemd, naar de vergelijking met de Union Jack
Voor ons probleem is dus $x^2+4=36+49$ , dus is $x=9$ .

Geplaatst in Kleine nootjes | Getagged brits flag theorem, Britse vlag stelling, kleine nootjes, problem solving, Pythagoras, union jack

Nootje 35

Geplaatst op 19 mei 2023 door admin

Zoek een getal van 6 cijfers dat begint en eindigt met een 2 en het product is van 3 opeenvolgende even getallen.

Antwoord

Even getallen eindigen steeds op 0,2,4,6 of 8.
Het product van drie opeenvolgende even getallen eindigt dan op $0*2*4$ , $2*4*6$ , $4*6*8$ of $6*8*0$ .
Enkel de combinatie $4*6*8$ eindigt dus op een 2.
Nu is $50^3=125000$ en $60^3=216000$ .
Bijgevolg zijn de getallen: 64,66 en 68 en hun product is 287232.

Geplaatst in Kleine nootjes | Getagged even getallen, problem solving

Nootje 33

Geplaatst op 13 mei 2023 door admin

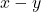Vind $x-y$ als gegeven is dat 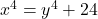$x^4=y^4+24$ , $x^2+y^2=6$ en $x+y=3$ .

Antwoord

Om de 2 onbekenden x en y uit te rekenen heb je eigenlijk maar 2 vergelijkingen nodig. Dan kan je ook $x-y$ uitrekenen. Maar waarschijnlijk is dat wel niet de bedoeling.
Omdat $x^4-y^4=(x-y)(x+y)(x^2+y^2)$ , vinden we uit de eerste betrekking dat $24=(x-y)*3*6$ ;
Hieruit volgt dan dat $x-y=\frac{4}{3}$ .

Geplaatst in Kleine nootjes | Getagged kleine nootjes, problem solving

Nootje 29

Geplaatst op 6 oktober 2022 door admin

Gegeven is een veelterm waarvan de coëfficiënten natuurlijke getallen zijn. Hoe kan je met zo weinig mogelijk evaluaties met natuurlijke getallen( berekenen van een getalwaarde) de coëfficiënten bepalen? Probeer eerst eens als alle coëfficiënten kleiner zijn dan 10.

Spoiler

Noem de veelterm P(x).
Als alle coëfficiënten kleiner zijn dan 10, volstaat 1 evaluatie. Bereken P(10).
Neem een voorbeeld als test: $P(x)=x^3+4x+8$ . Dan is $P(10)=10^3+4*10+8=1048$ . In deze uitkomst kan je de coëfficiënten inderdaad aflezen.
Wat nu als de de bovengrens van 10 niet meer geldig is. Dan hebben we 2 evaluaties nodig.
De eerste evaluatie dient om de bovengrens van de coëfficiënten te bepalen. Bereken P(1). Dan bestaat er een natuurlijk getal k zodat $P(1)<10^k$ . Bijgevolg is elke coëfficiënt kleiner dan $10^k$ .
De tweede evaluatie is dan $P(10^k)$ .
Testje? Neem $P(x)=12x^3+145x+88$ . dan is $P(1)=245<10^3$ . Neem $k=3$ en bereken $P(10^3)$ . Dit geeft 12.000.145.088. Opgedeeld in vakjes van $k=3$ cijfers krijgen we de gevraagde coëfficiënten.

Geplaatst in Kleine nootjes | Getagged getalwaarde veeltermen, kleine nootjes, problem solving, veeltermen

Opgave 36

Geplaatst op 26 september 2022 door admin

Wanneer deelt een natuurlijk getal n de uitdrukking $10^k-1$ voor een natuurlijke k?

Spoiler

Als n een veelvoud is van 2 of 5, dan is de enige mogelijkheid de triviale oplossing k=0.
Veronderstel dus verder dat n geen priemfactor 2 of 5 bevat.
Noteer met K(n) de kleinste, van 0 verschillende waarde van k, waarvoor $n|(10^k-1)$ .
Proberen we een aantal waarden uit:
$\begin{array}{c|c} n&K(n) \\ \hline \\ 3&1\\7&6\\9&1\\11&2 \end{array}$
Stel nu dat n, geen priemfactor 2 of 5 bevat, en een deler is van $10^k-1$ , dan bestaat er een natuurlijk getal a zodat $n.a=10^k-1$ .
Noteer de decimale schrijfwijze van a als $a=a_110^{k-1}+\cdots+a_{k-1}10+a_k$ .
Dan is $a_110^{k-1}+\cdots+a_{k-1}10+a_k=\frac{10^k}{n}-\frac{1}{n}$ .
Bij deling, van deze laatste vergelijking door $10^k$ vinden we:
$0,a_1\cdots a_{k-1}a_k=\frac{1}{n}-\frac{10^{-k}}{n}$
Als we steeds maar opnieuw delen door $10^k$ en alle bekomen formules lid per lid bij elkaar optellen vinden we
$\frac{1}{n}=0,a_1\cdots a_{k-1}a_ka_1\cdots a_{k-1}a_k\cdots$
Omgekeerd is het eenvoudig te zien dat, als $\frac{1}{n}$ een decimale ontwikkeling zoals hierboven heeft, dat n een deler is van $10^k-1$ .
Besluit: Als n geen priemfactor 2 of 5 bevat, dan in K(n) gelijk aan de lengte van de periode van $\frac{1}{n}$ .
Natuurlijk is elk veelvoud van k ook een goede oplossing.