Tag archieven: probleem oplossend denken
Opgave 15
Zoek het algemeen voorschrift van de rij 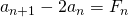 met
met 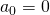 , waarbij
, waarbij  de rij van Fibonacci is met
de rij van Fibonacci is met 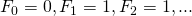
Opgave 14
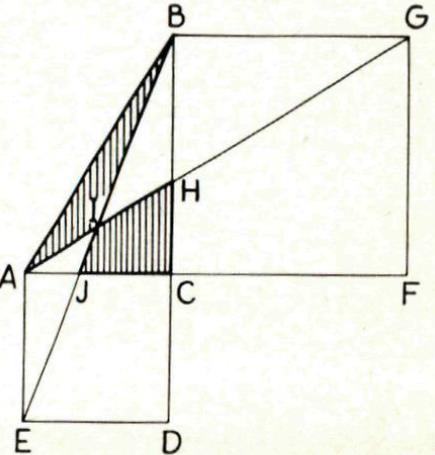
Op de zijden van een rechthoekige driehoek ABC tekent men twee vierkanten: BGFC en AEDC. De rechten AG en BE snijden elkaar in I. Verder is H het snijpunt van AG met BC en J het snijpunt van BE met AC. Bewijs dat de oppervlakte van ABI gelijk is aan de oppervlakte van IHJC.
Invariantieprincipe
De problemen die we nu zullen bestuderen gaan over processen die zich in een aantal toestanden kunnen bevinden. Laten we voor een gegeven probleem die toestanden even ![]() noemen. De overgang van de ene toestand naar de andere toestand is eenduidig vastgelegd door een aantal spelregels. Uiteindelijk is de vraag of het mogelijk is van toestand
noemen. De overgang van de ene toestand naar de andere toestand is eenduidig vastgelegd door een aantal spelregels. Uiteindelijk is de vraag of het mogelijk is van toestand ![]() naar een eindtoestand
naar een eindtoestand ![]() te gaan door de regels te gebruiken. Een strategie om aan te tonen dat dit onmogelijk is, is gebruik te maken van een functie f die gedefinieerd is op de verschillende toestanden van het probleem en die bij de overgang van de ene toestand naar de andere niet van waarde verandert. De functie blijft invariant gedurende het hele proces. Als uiteindelijk blijkt dat
te gaan door de regels te gebruiken. Een strategie om aan te tonen dat dit onmogelijk is, is gebruik te maken van een functie f die gedefinieerd is op de verschillende toestanden van het probleem en die bij de overgang van de ene toestand naar de andere niet van waarde verandert. De functie blijft invariant gedurende het hele proces. Als uiteindelijk blijkt dat ![]() kunnen we besluiten dat het onmogelijk is om van de begintoestand naar de eindtoestand te komen door gebruik te maken van de spelregels.
kunnen we besluiten dat het onmogelijk is om van de begintoestand naar de eindtoestand te komen door gebruik te maken van de spelregels.
Een voorbeeld:
Een draak heeft 100 hoofden. Een ridder kan er 15,17,20 of 5 afhakken. maar als hij dat doet, dan groeien er onmiddellijk 24,2,14 of 17 nieuwe hoofden bij. Als alle hoofden er af zijn dan is de draad dood. Kan de ridder de draak doden?
Heuristiek : Blikwissel
Door onze wiskundige ervaring beperken we ons soms tot die oplossingsmethoden die in het verleden steeds gewerkt hebben. Daardoor zie je soms een eenvoudige uitkomst over het hoofd. Een belangrijke heuristiek is bijgevolg: het probleem op een andere manier bekijken. We noemen dit blikwissel.
We doen alsof we de oplossing hebben en werken zo terug tot we terechtkomen bij een situatie die we wel meester zijn. We proberen een omgekeerde redenering op te zetten door van achter naar voor werken. We leven ons in in de personen, dieren, zaken die in de vraag voorkomen en bekijken het probleem eens vanuit hun standpunt. We kijken naar andere dingen, die niet rechtstreeks gevraagd zijn. We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn.
Bekijken we volgend voorbeeld:
Je beschikt over twee emmers, één van 9 liter en een van 4 liter. Hoe kan je hiermee precies 6 liter water uit een waterput afmeten?
We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn. Om 6 liter in de emmer van 9 liter over te houden, willen we die helemaal vullen en er 3 liter uit wegnemen. Dit lukt als we in de kleine emmer 1 liter water hebben staan. Hoe kunnen we nu 1 liter maken met deze twee emmers? Nu is ![]() . Onze strategie is dus:
. Onze strategie is dus:
- Vul de grote emmer.
- Vul hiermee de kleine emmer en ledig die. Je hebt dus 4 liter uit de grote emmer weggegoten.
- Giet nogmaals 4 liter van de grote emmer in de kleine en ledig die weer.
- Giet de overblijvende liter in de kleine emmer.
- Vul de grote emmer met 9 liter.
- Giet van de grote emmer zoveel water over tot de kleine emmer helemaal gevuld is.
- Nu blijft er 6 liter over in de grote emmer.

![Rendered by QuickLaTeX.com \[\begin{cases} n \equiv 0,1,2,3,4,5,6 \text{ mod } 9 \\ n \equiv 0,1,2,3,4,5,6 ,8,9,10,12,13,14 \text{ mod } 16\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-bdd2e4010102ab0476ddcbbad926ea37_l3.png?media=1678572382)