Tag archieven: primorial

Priemfaculteit

Geplaatst op door

Veronderstel dat p een priemgetal is. Definieer dan priemfaculteit p, genoteerd als p#, als het product van alle priemgetallen kleiner dan of gelijk aan p. Een paar voorbeelden.

    \[\begin{array}{c|r} p&p\#\\ \hline 2&2\\3&6\\5&30\\7&210\\11&2310 \end{array}\]

Men kan deze definitie uitbreiden voor niet priemgetallen. Zo is n# het product van alle priemgetallen kleiner dan n, als n niet priem is. Bijgevolg is, bijvoorbeeld, 7#=8#=9#=10#= 210.

Onderstaande grafiek geeft de waarde van n! en n# grafisch weer: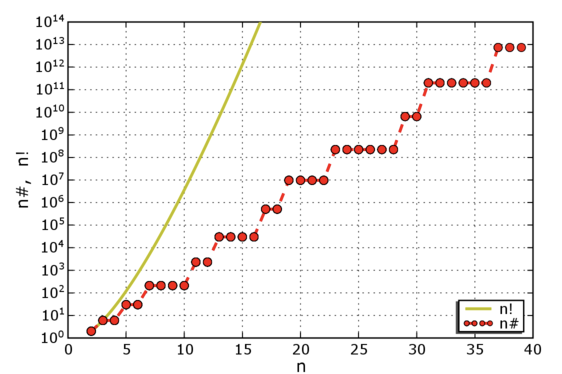

 

 

 

 

 

 

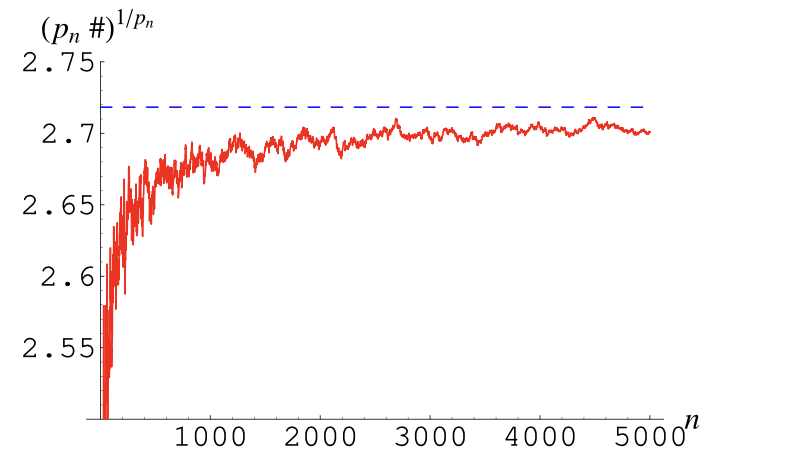
Verder is ook volgende eigenschap belangrijk: als n steeds maar toeneemt, zal (p\#)^{\frac{1}{n}} convergeren naar het getal van Euler: e