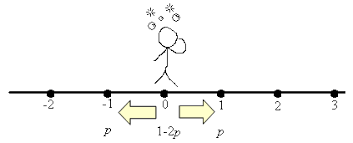
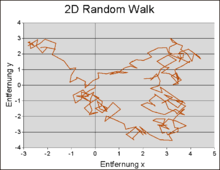
We bestuderen enkele eenvoudige stochastische wandelingen in d = 1,2 of 3 dimensies. Hier beweegt een fictieve wandelaar over het rooster door vanuit een punt naar één van de 2d buurpunten te lopen. Bij elke stap die hij doet zijn alle 2d richtingen even waarschijnlijk. Bovendien zijn alle stappen onafhankelijk van elkaar. De stochastische wandeling wordt ook wel eens de dronkemanswandeling genoemd, omdat de stappen van een (echt) dronken man goed gemodelleerd zouden kunnen worden met toevallige gebeurtenissen.

We onderzoeken de  stelling van Polya die zegt dat het deeltje zeker terugkomt naar de beginpositie enkel en alleen als de wandeling gebeurt in 1 of 2 dimensies. De stelling van Pólya is ook wel eens als volgt geformuleerd: a drunken man will always come home, but a drunken bird never will. Lees meer hierover in volgende tekst.