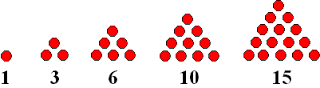
Hierboven zie je de eerste 5 driehoeksgetallen. Kan je nu de volgende vragen beantwoorden?

1. Als n een driehoeksgetal is, bewijs dan dan 8n+1 een volkomen kwadraat is.
   ( Plutarchus , 100 BC)
2. De som van twee opeenvolgende driehoeksgetallen is altijd een volkomen kwadraat. Bewijs. ( Nicomachus, 100 BC)
3. Als n een driehoeksgetal is, bewijs dan dat 9n+1 en 25n+3 ook driehoeksgetallen zijn. ( Euler, 1775)

Antwoorden Vraag 1

Een driehoeksgetal is de som van opeenvolgende natuurlijke getallen, beginnend met 1. Dus het n-de driehoeksgetal wordt gegeven door . Maar dan is . Bijgevolg is een volkomen kwadraat.

Antwoorden Vraag 2

Gebruikmakend van vorige formule is . Dus is . De som van twee opeenvolgende driehoeksgetallen is dus inderdaad een volkomen kwadraat.

Antwoorden Vraag 3

Stel . Dan is . Dus . Analoog is .