Tag archieven: plimpton 322

3.Wiskunde in Mesopotamië

Geplaatst op door

 

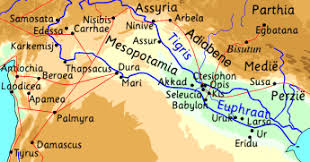
Mesopotamië wordt beschouwd als de bakermat van onze beschaving: het schrift, het wiel en de woonentiteit, die we nu ‘stad’ noemen, waren uitvindingen van de verschillende beschavingen die achtereenvolgens het gebied beheersten: Soemerë, Ur, Akkad en Babylonië. 

Het Mesopotamisch numeriek systeem is zestigdelig en positioneel:

POSITIONEEL : De cijfers van 1 tot 59 werden voorgesteld door een combinatie van 2 symbolen: het eenheidssymbool en het tien-symbool. 

ZESTIGDELIG : 1.60³+57.60²+46.60+40 = 424000

 

Het getal 0 kenden ze niet. Optellen en aftrekken ging erg vlot. Het vermenigvuldigen had wat meer voeten in de aarde. In ons tientallig stelsel, moeten de tafels tot en met 9 bekend zijn om te kunnen vermenigvuldigen.  Doordat ze echter gebruik maakten van een zestigtallig stelsel moesten alle tafels tot en met 59 bekend zijn om verder te rekenen. Zij hadden per tafel 23 producten nodig: van 1 tot en met 20, 30, 40 en 50. In totaal dus 59 × 23 = 1357 producten. Er zijn ook kleitabletten met hierop de kwadraten van 1 tot en met 59 gevonden.  Door gebruik te maken van de formule :

    \[a.b = \frac{1}{2}\Big((a+b)^2-a^2-b^2\Big)\]

 

    \[a.b=\frac{1}{4}\Big((a+b)^2-(a-b)^2\Big)\]

konden ze via de tabellen met kwadraten ook vermenigvuldigingen uitvoeren. Om een deling uit te voeren hadden ze een tabel waarin de omgekeerden stonden van hun basisgetallen.

Lange tijd werd gedacht dat de Babyloniërs niet aan meetkunde deden, maar alleen rekenden om bijvoorbeeld voedselvoorraden bij te houden. maar men heeft kleitabletten gevonden waar twee intervallen op staan wanneer Jupiter aan de horizon verschijnt. De positie van de planeet wordt berekend op zestig en honderdtwintig dagen. De tekst bevat geometrische berekeningen gebaseerd op het oppervlak van een trapezium met lange en korte zijden.

 

We geven een paar voorbeelden uit de praktijk van de Babylonische wiskunde:

  • Een methode om de verhouding van de diagonaal tot de zijde van een vierkant te berekenen: Een vierkant met zijde 30 heeft een diagonaal 42;25,35. Daaruit wordt de verhouding van de diagonaal tot de zijde berekend als 1;24,51,10 of omgerekend in ons tiendelig stelsel 1,4142130 wat ongeveer de vierkantswortel uit 2 is.


  • Pythagorese drietallen  in het tablet Plimton 322: