Het groeimodel van Malthus voorspelt een exponentiële groei. In de praktijk zijn er echter grenzen aan de bevolkingsexplosie, doordat bijvoorbeeld de woonomgeving of de voedselsituatie een begrenzing stelt op de grootte van de populatie.

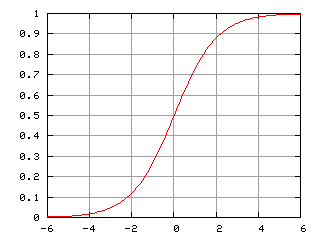
Pierre Verhulst(1804-1849), een Belgisch mathematisch bioloog modelleerde dit als volgt:

   

waarbij N(t) de grootte van de populatie weergeeft op elk tijdstip t. Op basis van zijn studie van de evolutie van de bevolkingscijfers leidde Verhulst af dat deze remmende factor evenredig is met het verschil tussen de populatie op een gegeven tijdstip en de maximale populatie M. De oplossing van deze differentiaalvergelijking geeft de bekende logistische functie met als grafiek de sigmoïde:

De logistische functie van Verhulst wordt tegenwoordig vooral gebruikt in biologische wetenschappen, bijvoorbeeld bij de studie van bacteriënpopulaties. Ook bij de besmettingscijfers van de Corona pandemie zie je deze grafiek terugkomen.