We kunnen elke breuk schrijven in zijn decimale vorm. Ofwel eindigt deze schrijfwijze ( niet repeterend) , zoals bij ofwel krijg je een deel dat zich steeds herhaalt ( repeterend). Neem bijvoorbeeld . De periode is 3 ( het deel dat herhaald wordt ) en de lengte van de periode is 1.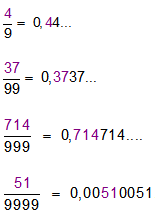

Hoe kunnen we nu de lengte van die periode berekenen?

• De teller van de breuk speelt geen rol bij de lengte van de periode. Vandaar dat we enkel  zullen werken met stambreuken .
• Een breuk is niet repeterend als de priemontbinding van de noemer enkel bestaat uit factoren 2 en 5.
• De lengte van de deel na de komma, voor het repeterend deel: kijk naar het aantal twee en het aantal vijven in de priemfactor ontbinding en neem het grootste aantal van beiden. Zo is :  dus 1 cijfer voor het repeterend deel begint.
• De lengte van de periode van is de kleinste p waarvoor geldt dat n een deler is van .
• Als n een priemgetal is dan is de lengte van de periode van een deler van n – 1. Als de lengte juist n – 1 is, dan noemen we dat priemgetal een volledig herhalend priemgetal. Onder 1000 zijn dat het getallen 7, 23, 47, 59, 167, 179, 263, 383, 503, 863, 887, 983.
• Als n en m priem zijn en de lengtes van de periodes van en 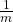zijn respectievelijk en , dan is de lengte van de periode van 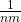het kleinste gemene veelvoud van en of een veelvoud daarvan.
• Als n een priemgetal is waarvan de lengte van de periode gelijk is aan p, dan is de lengte van  de periode van gelijk aan .

Een voorbeeld: Neem de breuk . De noemer is te schrijven als . De lengte van de periode voor een noemer 19 is een deler van 18 en narekenen leert ons dat het 18 is. De lengte van de periode voor een noemer 31 is een deler van 30 en blijkt 15 te zijn. Vervolgens nemen we het kleinste gemene veelvoud van 18 en 15: dit is 60. Bijgevolg is de lengte van de periode van gelijk aan 90.