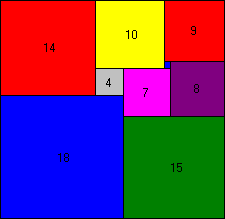
Een rechthoek R die kan verdeeld worden in verschillende vierkanten van verschillende grootte,  noemt men een perfecte rechthoek. Zo een verdeling noemt men vierkansverdeling van orde n als er n verschillende vierkanten gebruikt worden.

Dit is een vierkansverdeling van orde 9 van een rechthoek van 32 bij 33. Deze verdeling werd gevonden door A Moron (1904-1971), een Pools wiskundige in 1925.

Lange tijd dacht men dat perfecte vierkanten niet bestonden.  Tot in 1939 de Duitse wiskundige R. Sprague een perfect vierkant vond van orde 55. Later , in 1940 hebben Reichert en Toepkin zelfs bewezen dat een perfect vierkant van een orde kleiner dan 9 niet bestaat. 

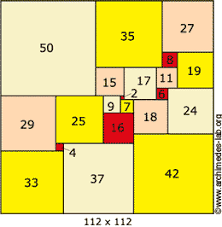
21 is de kleinste orde voor een perfect vierkant. Hieronder zie je een perfect vierkant met een unieke 21 vierkansverdeling . Is de orde hoger dan 21, dan zijn er meerder vierkanten mogelijk; zo zijn er bijvoorbeeld 441 perfecte vierkanten van orde 26.