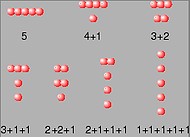
Hoeveel snoeren kan je maken met 3 rode en 5 witte kralen? Als je het snoer draait (cyclisch) of omkeert ( spiegeling), krijg je geen ander snoer.
We stellen een snoer voor als een combinatie van 3 R-en en 5 W’s. We weten dat WRRRWWWW en RRRWWWWW dezelfde ketting voorstelt. We kunnen er dus steeds voor zorgen dat we eindigen met een R. Maar ook RRWRWWWW en RWRRWWWW stellen hetzelfde snoer voor, want als je de laatste 4 W’s vooraan zet, zijn de twee snoeren elkaars spiegelbeeld.
Focussen we ons even op de rode kralen en bekijken we een snoer als
…R…R…R, dan rest ons de 5 witte kralen te verdelen over de drie aangegeven vakjes (na de laatste R is er geen vakje meer wegens het cyclisch zijn van het snoer. We coderen het snoer door de aantallen witte kralen in die vakjes. De combinatie WRRRWWWW en RRRWWWWW of WWWWWRRR stellen we dan voor als 500 en de gelijke snoeren RRWRWWWW en RWRRWWWW worden dan 401 en 410. We kiezen voor die getallencombinatie die een niet -stijgende rij is.
Welke mogelijkheden houden we uiteindelijk over?
RRRWWWWW=500
RRWRWWWW=401=410
RRWWRWWW=302=320
WRWRWWWR=113=311
WRWWRWWR=122=221
En dus is het aantal snoeren gelijk aan het aantal partities van 5 in hoogstens 3 delen, dit is het aantal manieren om 5 te schrijven als de som van hoogstens 3 postieve getallen. Kunnen we dit veralgemenen? 3 rode en n witte kralen? Lees hierover meer in volgens artikel.