Tag archieven: paradox

De wielparadox

Geplaatst op door

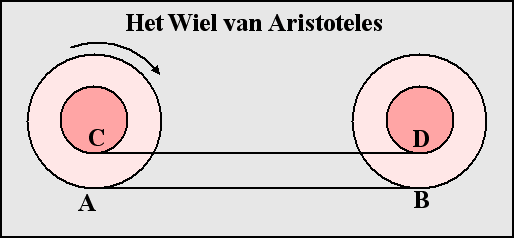
Stelt u zich een klein wiel op een groot wiel voor, voorgesteld als twee concentrische cirkels. Voor elk punt op de kleine cirkel is er exact één punt op de grote cirkel en omgekeerd.Je kan dus verwachten dat het samengestelde wiel dezelfde afstand aflegt als het kleine wiel over een staaf rolt of als het grote wiel over de weg rolt. Maar dat kan toch niet, want de omtrek van beide cirkels is verschillend!

Deze paradox werd door Aristoteles beschreven in een oude Griekse tekst Mechanica. 

Cantor heeft veel later aangetoond dat een een-op-eenovereenkomst van punten, niet betekent dat twee krommen even lang moeten zijn. 

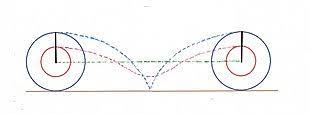
De totale verplaatsing van punten op de omtrek van een Aristoteles-wiel kan je zien op onderstaande afbeelding:

De trompet van Torricelli

Geplaatst op door

De buis van Torricelli is een driedimensionale figuur uitgevonden door Evangelista Torricelli( 1608-1647). Het ontstaat door y=\frac{1}{x} te wentelen rond de X-as voor x\geq1.

De figuur is speciaal omdat de oppervlakte ervan oneindig is, terwijl de inhoud eindig is. Stel dat je de binnenkant van de trompet wil schilderen, dan lijkt dat een onbegonnen zaak omdat de oppervlakte die je dan moet schilderen oneindig groot is. Zet de trompet op zijn zijkant en vul ze volledig met verf (inhoud = eindig!). Dan is de binnenkant ineens mee geschilderd, toch?

De naam verwijst naar het religieuze verhaal van de Dag des oordeels, waarop de aartsengel Gabriël op de trompet blaast. Hierbij wordt het oneindige gelinkt aan het goddelijke.

De paradox van Bertrand

Geplaatst op door

Sinds Zeno aantoonde dat de snelvoetige Achilles de schildpad nooit zou inhalen, hebben vele paradoxen de wiskundige gemeenschap bezig gehouden. Elke paradox draagt bij tot een dieper inzicht in de wiskunde die men bedrijft.

Ook de kanstheorie is niet gespaard gebleven van haar portie paradoxen. Begin vorige eeuw waren verschillende wiskundigen zich bewust van bepaalde problemen bij het berekenen van kansen. Onder andere Joseph Bertrand( Franse wiskundige, die leefde van 1822 tot 1900) wilde beklemtonen dat een degelijke fundering van verscheidene, intuïtief gebruikte begrippen noodzakelijk was. Het was wachten tot 1933 om via het monumentale werk van A.N.Kolmogorov te ontdekken dat de ideale axiomatische theorie voor de kansrekening die der maattheorie is.

Besluit: een uitspraak in kanstheorie heeft enkel zin met betrekking tot een bepaalde kansruimte, in het bijzonder met betrekking tot een bepaald universum.

 

Lees hier meer over het koordenprobleem van Bertrand.