Elke groep G werkt, door toevoeging, op zichzelf: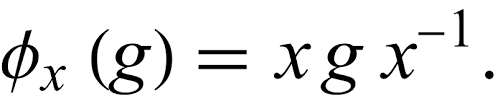

De baan van een element x van G, ook orbit genoemd, noteren we als Orb(x) en is de verzameling elementen van G die toegevoegd zijn aan x: met andere woorden de toevoegingsklasse van x.

De centralisator   van een element g is de verzameling elementen van G die commuteren met g. Het is altijd een deelgroep van G en er is een bijectief  verband tussen de elementen van  Orb(x) en . Met andere woorden de orde van een toevoegingsklasse is de index van de centralisator van een willekeurig element x van die klasse in G. Dus deelt de orde van een toevoegingsklasse steeds de orde van de groep.

De klassen vergelijking schrijft de orde van G als som van de ordes van de toevoegingsklassen.