Wiskunde is leuk

Nootje 36

Geplaatst op 27 mei 2023 door admin

Vind alle niet complexe oplossingen van
$(2x+1)(3x+1)(5x+1)(30x+1)=10$

Antwoord

Alles uitrekenen geeft een vierdegraadsvergelijking, die waarschijnlijk niet op te lossen is.
We gaan de factoren in het linkerlid twee per twee uitrekenen: de eerst met de laatste en de twee middelsten.
De opgave wordt dan: $(15x^2+8x+1)(60x^2+32x+1)=10$ .
We merken op dat de twee eerste termen van de tweede factor het viervoud zijn van de eerste twee termen van de eerste factor. Stel $15x^2+8x=y$
We krijgen dan $(y+1)(4y+1)=10$ of na uitwerken $4y^2+5y-9=0$ .
Deze vierkantsvergelijking heeft als oplossingen 1 en $-2,25$ .
Vervangen we y terug dan verkrijgen we twee vergelijkingen van de tweede graad. De eerste 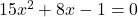$15x^2+8x-1=0$ geeft als oplossingen $\frac{-4\pm \sqrt{31}}{15}$ .
De tweede vergelijking wordt 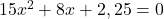$15x^2+8x+2,25=0$ en deze heeft geen reële oplossingen.
De enige niet complexe oplossingen zijn dus
$\frac{-4\pm \sqrt{31}}{15}$

Gebruikmaken van de symmetrie

Geplaatst op 10 september 2017 door admin

Soms kan je, door gebruik te maken van de symmetrie in de tekening of de symmetrie van de gegevens, de opgave aanzienlijk vereenvoudigen.

Een voorbeeld: Los op in $\mathbb{R}$ :

$(x+2013)(x+2014)(x+2020)(x+2021)=44$

Dit is een vierdegraads vergelijking. Hiervoor kennen we geen algemene oplossingsmethode.
Dus: haakjes uitwerken en dan ofwel proberen te ontbinden in factoren ofwel de regel van Horner toepassen. Maar dit is niet aantrekkelijk want de getallen in de opgave zijn nogal groot.
De getallen 2013,2014,2020 en 2021 liggen wel symmetrisch rond 2017!
We vervangen $x+2017$ door een nieuwe variabele $t$ . De opgave wordt nu:
$(t-4)(t-3)(t+3)(t+4)=44$

.
Dit kan je netjes uitrekenen tot:
$(t^2-16)(t^2-9)=44$
Verder uitrekenen geeft: $t^4-25t+100=0$ . Hieruit volgt dat $t^2=20$ of $t^2=5$ .
De 4 oplossingen voor $t$ zijn dan: $\pm \sqrt{5}$ en $\pm \sqrt{20}$ . En dus moet \newline $x=-2017 \pm \sqrt{5}$ of $x=-2017 \pm \sqrt{20}$ .