Tag archieven: ontbinding in factoren

Les 4: ontbinding en exhaustie

Geplaatst op door

Bij Diophantische vergelijkingen van een hogere graad kan je via ontbinding in factoren dikwijls de oplossing vinden. Neem bijvoorbeeld:

    \[3x^2-4xy+5=0\]

  • We kunnen deze vergelijking herschrijven als

        \[x(3x-4y)=-5\]

  • Als x en y gehele getallen zijn, dan moeten x en 3x-4y delers zijn van -5.
  • We kunnen gemakkelijk alle mogelijkheden opschrijven: 

        \[\begin{array}{c|c|c} x&3x-4y&y \\ \hline \\1&-5&2\\-1&5&-2\\5&-1&4\\-5&1&-4\end{array}\]

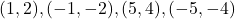  • We hebben dus als oplossingen (1,2),(-1,-2),(5,4),(-5,-4).

 

Nootje 12

Geplaatst op door

a,b,c,d en e zijn 5 verschillende gehele getallen zodat hun product 45 is. Wat is dan hun som?

Antwoord

  • We weten dat 45 = 3 x 3 x 5.
  • Om dat we 45 schrijven als een product van 5 verschillende getallen moeten elk van zijn priemfactoren voorkomen en ook \pm 1.
  • -3 en -1,  mogen maar 1 keer voorkomen, dus is

        \[45=(-1) \times 1 \times (-3) \times 3 \times 5\]

  • De som van die 5 getallen is dan 5.