We weten dat n! = n.(n-1)…1. We willen nu onderzoeken wat de exponent is van een priemgetal p in de ontbinding in factoren van n!
- Schrijf n in het p-tallig stelsel:
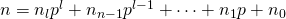 .
.
- Elk veelvoud van p tussen 1 en n levert 1 factor p in de ontbinding van n!. Zo zijn er
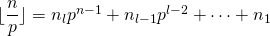 , want
, want 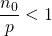 .
.
- Elk veelvoud van
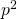 tussen 1 en n levert een extra factor p in de ontbinding van n!. Zo zijn er
tussen 1 en n levert een extra factor p in de ontbinding van n!. Zo zijn er 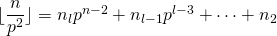 , want
, want 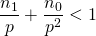
- Noteer met
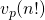 de exponent van p in de ontbinding van n!.
de exponent van p in de ontbinding van n!.
- Dan is:
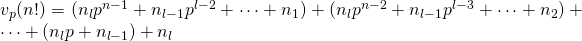
- Herschikking geeft:

- Dus
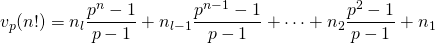 .
.
- Noteer
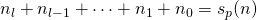 .
.
- Bijgevolg is
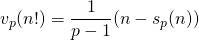 .
.
Voorbeeld : ![]()
- 12 = 1100 in het binair talstelsel, dus is
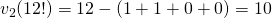 .
. - 12 = 110 in het drietallig stelsel, dus is
 .
. - 12 = 22 in het vijftallig stelsel , dus is
 .
. - 12 = 15 in het zeventallig stelsel , dus is
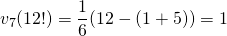 .
. - 12 = 11 in het elftallig stelsel , dus is
 .
.
