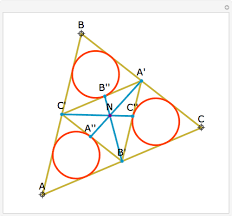
De middendriehoek van een driehoek ABC is de driehoek SRQ, gevormd door de middenparallellen van de gegeven driehoek. 

Enkele eigenschappen:

• De oppervlakte van de middendriehoek is van de oppervlakte van de gegeven driehoek.
• De omtrek van de middendriehoek is 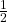van de omtrek van de gegeven driehoek.
• De middendriehoek  is gelijkvormig met de gegeven driehoek: de middendriehoek is het beeld van ABC onder een homothetie met centrum het zwaartepunt van ABC en als factor .
• De middendriehoek en driehoek ABC hebben hetzelfde zwaartepunt.
• Het hoogtepunt van de middendriehoek valt samen met het middelpunt van de omgeschreven cirkel van driehoek ABC.
  
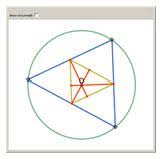
• De voetpunten van de hoogtelijnen van driehoek ABC liggen op de omgeschreven cirkel van de middendriehoek.
  
  
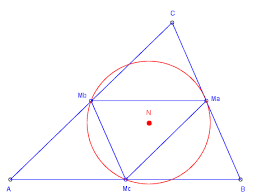
• De omgeschreven cirkel van de middendriehoek is de negenpuntscirkel van ABC ( de cirkel door de middens van de zijden, de voetpunten van de hoogtelijnen en de middens van de lijnsegmenten van uit de hoekpunten naar het hoogtepunt ).
  
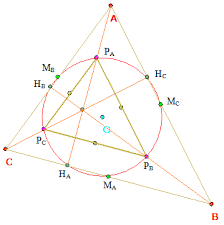
• En dan nog deze afsluiter: bedenk zelf maar de stelling!