Tag archieven: menelaos

Griekse wiskunde : deel 9

Geplaatst op door

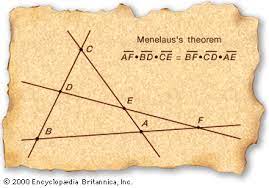
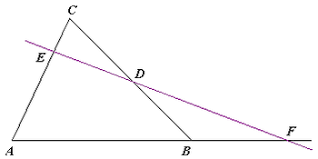
Na Apollonius begint voor de Griekse meetkunde een periode van stagnatie en verval. Personen zoals Heron van Alexandrië (1ste eeuw NC), Menelaos van Alexandrië(1ste eeuw NC), Theon van Alexandrië(4e eeuw NC), Proclus en Pappus leveren weinig nieuwe bijdragen , maar brengen hoofdzakelijk commentaren op en aanvullingen van de werken van de oude meesters. De laatste Alexandrijnse wiskundige is Hypatia, de eerste bekende vrouwelijke wiskundige.

De voornaamste redenen van de teleurgang van de Griekse meetkunde zijn:

  • Het gebrek aan belangstelling van de Romeinse keizers voor de zuivere wetenschappen.
  • De uitbuiting van de Hellenistische landen door de Romeinen, waardoor het wetenschappelijk onderzoek niet langer financieel gesteund werd.
  • Het ontbreken van zuiver-algebraïsche methodes ( en vooral symbolen) waardoor een verdere ontwikkeling bemoeilijkt wordt.

De stellingen van Ceva en Menelaos

Geplaatst op door

Pareltjes uit de oude doos!

De stelling van Ceva zegt : AD, BE en CF snijden elkaar is 1 punt is equivalent met

    \[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=1\]

Hierbij moeten de verhoudingen opgevat worden als verhoudingen van de overeenkomstige vectoren, zodat de verhouding negatief is als de vectoren tegengesteld zijn. De transversalen AD, BE en CF  worden ook wel Cevianen genoemd. De stelling werd voor het eerst bewezen door Giovanni Ceva in zijn werk De lineis rectis uit 1678. 

Als we stelling van Ceva ‘vertalen’ (  punt wordt lijn en lijn wordt punt, lijn gaat door punt wordt punt ligt op lijn, snijpunt van 2 lijnen wordt verbindingslijnstuk van 2 punten) krijgen we de stelling van Menelaos:

Drie punten, D,E en F, gelegen op de zijden van een driehoek, liggen op één lijn als en slechts als 

    \[\dfrac{|AF|}{|FB|}.\dfrac{|BD|}{|DC|}.\dfrac{|CE|}{|EA|}=-1\]

Merk op dat de verhouding positief is als F tussen A en B ligt, en negatief als F buiten het lijnstuk AB ligt.