Tag archieven: meetkunde

De stelling van Napoleon

Geplaatst op door

Iedereen kent gelijkvormige driehoeken. In deze tekst proberen we ze te beschrijven met complexe getallen. Elk punt Z in het vlak correspondeert met een uniek complex getal z.

Twee driehoeken ABC en DEF zijn rechtstreeks gelijkvormig ( alle  hoeken hebben eenzelfde oriëntatie, bvb met de klok mee) als en slechts als

    \[\begin{vmatrix} a&d&1\\b&e&1\\c&f&1 \end{vmatrix}=0\]

Bij onrechtstreekse gelijkvormigheid moet je , in de tweede kolom, elk complex getal vervangen door zijn complex toegevoegde. Gebruiken we deze formules nu op een voorbeeld:

De stelling van Napoleon luidt dat als aan de zijden van een willekeurige driehoek gelijkzijdige driehoeken worden vastgemaakt, ofwel alle drie naar buiten, ofwel naar binnen gericht, dat vormen de zwaartepunten van die driehoeken  een gelijkzijdige driehoek.

  • We veronderstellen alle driehoeken klok georiënteerd.
  • Elke gelijkzijdige driehoek is gelijkvormig met de driehoek gevormd door de complexe getallen 1,\omega en \omega^2 . Hierbij is \omega=\frac{-1+\sqrt{3}i}{2}.
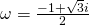  • Als ABC gelijkzijdig is dan moet

        \[a+b\omega+c\omega^2=0\]

    Dit volgt uit vorige opmerking.

  • Dus is :

        \[\begin{array}{c} c+x\omega+b\omega^2=0\\b+z\omega+a\omega^2=0\\a+y\omega+c\omega^2=0\end{array}\]

  • Door de tweede vergelijking te vermenigvuldigen met \omega en de derde met \omega^2 vinden we:

        \[\begin{array}{c} c+x\omega+b\omega^2=0\\a+b\omega+z\omega^2=0\\y+c\omega+a\omega^2=0\end{array}\]

  • Omdat M,L en N zwaartepunten zijn geldt: 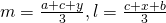m=\frac{a+c+y}{3},l=\frac{c+x+b}{3} en n=\frac{a+b+z}{3}.
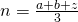  • Rest ons te bewijzen dat MLN gelijkzijdig is, daartoe moeten we bewijzen dat m+l\omega+n\omega^2=0. Een combinatie van de twee laatste puntjes geeft ons het gewenste resultaat.

Bewijs zonder woorden

Geplaatst op door

We maken gebruik van volgende stellingen:

  • De sinusregel die zegt dat sin x = 2R .a waarbij a de zijde is tegenover hoek x en waarbij R de straal is van de omgeschreven cirkel. Zo bepalen we in de tekening de zijden met lengte sin x, sin y en
    p = sin (x + y).
  • Een omtrekshoek op een halve cirkel is recht. In combinatie met vorig punt vinden we zo de zijden met lengte cos x en cos y.
  • In een koordenvierhoek is de som van de producten van de overstaande zijden gelijk aan het product van de diagonalen. Zo vinden we een uitdrukking voor p.

De ongelijkheid van Euler

Geplaatst op door

Eén van de oudste ongelijkheden in een driehoek is de ongelijkheid van Euler die een verband geeft tussen de stralen van de omgeschreven en ingeschreven cirkel.

Als O het middelpunt is van de omgeschreven cirkel ( met straal R) van driehoek ABC en I het middelpunt van de ingeschreven cirkel (met straal r), noteer dan d=|OI|. Dan geldt er:

    \[d^2=R^2-2Rr\]

Hieruit volgt dan dat

    \[R\geq 2r\]

Het gelijkheidsteken geldt enkel als de driehoek gelijkzijdig is.

Een meetkundige plaats

Geplaatst op door

Gegeven is een cirkel met middelpunt A en straal R en een punt B buiten de cirkel. Neem een willekeurig punt Q op die cirkel en bereken het snijpunt P van QA met de middelloodlijn van QB. Bepaal de meetkundige plaats van de punten P als Q zich op d ecirkel beweegt.

  • We schakelen Geogebra in om een inpressie te krijgen van die meetkundige plaats:
  • De oplossing lijkt een hyperbool te zijn. Omdat P op de middelloodlijn van QB ligt is |PQ|=|PB| en bijgevolg is |PA|+R=|PB| of

        \[|PB|-|PA|=R\]

    Het verschil van de afstanden van P tot twee vaste punten A en B is dus constant en daarom is de meetkundige plaats inderdaad een hyperbool.

  • In de tekening zijn ook de raaklijnen uit B aan de cirkel getekent ( met raakpunten D en E). Als Q samenvalt met D of E dan bestaat P niet, omdat QA dan loodrecht staat op QB en dus evenwijdig is met de middelloodlijn.
  • Als Q samenvalt met de snijpunten van AB met de cirkel, dan vinden we de toppen van de hyperbool.
  • Als Q de grote boog DE doorloopt, dan vinden we de linkertak van de hyperbool. Het andere deel van de cirkel coorespondeert dan met de rechtertak.

Een vlieger

Geplaatst op door

 

 

Een vlieger is een meetkundige figuur waar bij exact twee overstaande hoeken, de aanliggende zijden gelijk zijn. Die hoekpunten noemt men de toppen van de vlieger. In onderstaande figuur zijn A en C de toppen.

Verdere eigenschappen:

  • De diagonalen staan loodrecht op elkaar.
  • De diagonaal door de toppen is de enige symmetrieas van de vlieger.
  • De overstaande hoeken, die niet bij de toppen horen, zijn gelijk.
  • De oppervlakte van de vlieger is het halve product van de lengtes van de diagonalen.
  • De diagonaal door de toppen deelt de andere diagonaal middendoor.
  • Een vlieger is een raaklijnen vierhoek en heeft dus een ingeschreven cirkel. In bovenstaande figuur is het middelpunt van de cirkel het snijpunt van de diagonaal door de toppen met de bissectrice van de hoek in D.