Wat is groter 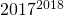 of
of  ?
?
Antwoord
- Noteer 2017 = x en 2018 = y, dan moeten we zoeken welke van de twee,
 of
of 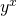 , het grootst is. Hierbij is
, het grootst is. Hierbij is  .
. - Als we zouden veronderstellen dat
 , dan is komt dit neer op
, dan is komt dit neer op 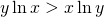 , want de natuurlijke logaritmische functie is stijgend.
, want de natuurlijke logaritmische functie is stijgend. - Dit is te herschrijven als :
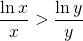 .
. - Daaro onderzoeken we de functie
 .
.  . Bijgevolg is
. Bijgevolg is 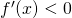 als
als  , en is f daar dalend.
, en is f daar dalend.
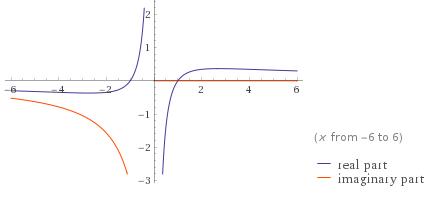
- Klaar! : Omdat
 en omdat f dalend is rechts van e, zal de volgorde van de beelden worden omgedraaid , dus
en omdat f dalend is rechts van e, zal de volgorde van de beelden worden omgedraaid , dus 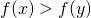 en bijgevolg is
en bijgevolg is
![Rendered by QuickLaTeX.com \[2017^{2018}>2018^{2017}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-5eae0bcd9b6cf2e5d02e1faaca07bdd7_l3.png?media=1678572382)

