Een mooie toepassing op de studie van lineaire vergelijkingen en ongelijkheden met 2 onbekenden is de lineaire programmering ( LP). Het gaat hier over  optimaliseringsproblemen waarin de doelfunctie en de randvoorwaarden allen lineair zijn. De methode van de lineaire programmering werd in 1939 voor het eerst door de Sovjet-Russische wiskundige Leonid Kantorovitsj besproken in zijn boek “Wiskundige methoden in de organisatie en planning van de productie“.

Mede voor dit werk kreeg Kantorovitsj in 1975 de Nobelprijs in de Economie. Bekijken we eens een voorbeeld:

Bepaal de extreme waarden van met als randvoorwaarden

(1)  

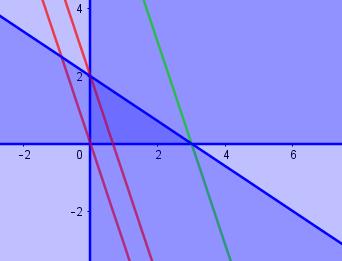
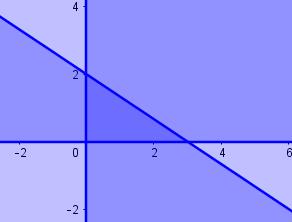
Eerst bepalen we grafisch de koppels die aan de randvoorwaarden voldoen. Dit gebied noemen we het aanvaardingsgebied. We vinden een rechthoekige driehoek ( donkerblauw gekleurd)
Vervolgens worden enkele niveaulijnen van de functie getekend. Dit zijn lijnen die alle punten , met een zelfde functiewaarde, met elkaar verbinden. Voor een lineaire functie zijn deze niveaulijnen altijd evenwijdige rechten. Bij het zoeken van de extreme waarden voor moeten we rekening houden met de randvoorwaarden. Grafisch betekent dit dat de lijnen door het aanvaardingsgebied moeten gaan. In onderstaande tekening hebben we en getekend ( rode rechten). Maar ( groene lijn ) is die lijn, onder alle evenwijdige lijnen, die het aanvaardingsgebied het meest naar rechts snijdt. Bijgevolg is 9  de maximale waarde voor de functie onder de gegeven randvoorwaarden.