Naast lineaire vergelijkingen , kunnen we ook lineaire congruenties bekijken:
![]()
Hier is de vraag of er een gehele x te vinden is zodat ![]() deelbaar is door m. Het is duidelijk dat als
deelbaar is door m. Het is duidelijk dat als ![]() een oplossing is, dan zijn alle getallen uit de restklasse
een oplossing is, dan zijn alle getallen uit de restklasse ![]() ook oplossingen. De oplossingsverzameling verandert ook niet als we a en b veranderen in andere getallen uit hun restklasse mod m. Onder een oplossing van een lineaire congruentie verstaat men dus een restklesse mod m.
ook oplossingen. De oplossingsverzameling verandert ook niet als we a en b veranderen in andere getallen uit hun restklasse mod m. Onder een oplossing van een lineaire congruentie verstaat men dus een restklesse mod m.
- Wanneer is een congruentie oplosbaar? Dat is zo als en slechts als de grootste gemene deler van a en m een deler is van b. Als a en m onderling ondeelbaar zijn, bestaat het inverse element van a mod m en is dus
 . Als de grootste gemene deler d van a en m niet 1 is , dan delen we eerst door d en dan krijgen we vorige situatie.
. Als de grootste gemene deler d van a en m niet 1 is , dan delen we eerst door d en dan krijgen we vorige situatie. - In het geval dat ggd(a,m) = 1 hebben we een unieke oplossing. Als echter ggd(a,m) = d , dan hebben we d oplossingen. We krijgen immers 1 oplossing mod
 en deze geeft precies volgende verschillende restklassen mod m:
en deze geeft precies volgende verschillende restklassen mod m:  .
.
Los op : ![]() .
.
- Delen door de ggd(6,10) = 2 geeft
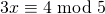 .
. - Omdat
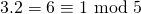 is
is 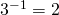
- En dus is
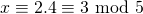 .
. - Alle oplossingen zijn dus de restklassen 3 en 8 modulo 10. De oplossingsverzameling is:
![Rendered by QuickLaTeX.com \[\{3+10k, 8+10l \text{ met } k,l\in \mathbb{Z}\}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-4d4dbf6d32e3319bd9351605d2f3a06c_l3.png?media=1678572382)
