Tag archieven: Lenstra

Priemgetaltest

Geplaatst op door

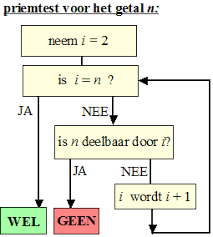
We willen twee fundamentele vragen uit de getaltheorie even onder de aandacht brengen:

  1. Hoe kan men snel zien of een getal een priemgetal is?
  2. Als n niet priem is, hoe vindt men gehele getallen a en b , groter dan 1, zodat n = a.b?

Het is verbazingwekkend dat men dikwijls kan weten dat een getal niet priem is, zonder er een factor van te kennen. Dat is te danken aan de stelling van Fermat: als n priem is dan geldt voor elk geheel getal a dat

    \[a^n \equiv a \mod n\]

Dus als je een geheel getal a kan vinden waarvoor a^n niet gelijk is aan a modulo n, dan weet men zeker dat n niet priem is, zonder nochtans een factor van n te kennen.

Willen we bewijzen dat een getal toch priem is, dan hebben we een omkering van de stelling  van Fermat nodig. Hier doen zich twee moeilijkheden voor:

  • De directe omkering is gewoon fout! Het getal n = 1729 = 7.13.19 is niet priem en toch is 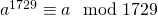 a^{1729}\equiv a \mod 1729 voor elk geheel getal a.
  • En zelfs al zou de omkering waar zijn, dan zou ons dat niet echt helpen want het is ondoenlijk alle gehele getallen a te proberen.

Het zoeken naar oplossingen van deze problemen is zeer actueel en de gevonden methoden zijn soms zelfs futuristisch, aangezien ze steunen op het nog onbewezen vermoeden betreffende de veralgemeende Riemannhypothese.  Enkele namen die op dit gebied een belangrijke bijdrage geleverd hebben zijn: R. Solovay, V.Strassen, G.L. Miller, M.O.Rabin en  H.W. Lenstra ( zie foto)