Tag archieven: krommen

De limaçon van Pascal

Geplaatst op door

Een andere voorbeeld van een ‘meetkundige’ kromme is de Limaçon van Pascal. 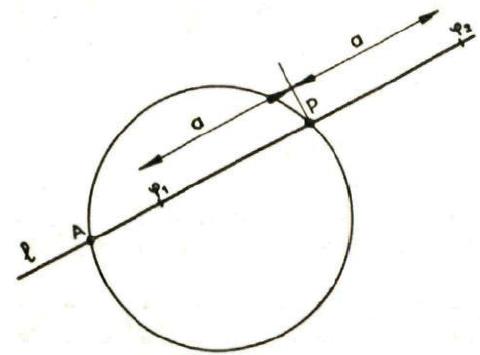Neem een willekeurig punt A op een cirkel met straal r. Teken door A een rechte l die de cirkel een tweede keer snijdt in P. Construeer 2 punten op l die op een afstand a van P liggen: Q_1 en Q_2. Bepaal de meetkundige plaats van deze punten als de rechte l rond A draait.

Neem de oorsprong van het assenstelsel in het middelpunt van de gegeven cirkel en de X-as door A. De rechte l heeft als vergelijking: y=\lambda (x-r). Het andere snijpunt van l met de gegeven cirkel is P(r.\dfrac{\lambda^2-1}{\lambda^2+1},-2r.\dfrac{\lambda}{\lambda^2+1}). Om de meetkundige plaats te kennen van de punten Q_1 en Q_2 moeten we \lambda elimineren uit y=\lambda (x-r) en uit de vergelijking van de cirkel met middelpunt P en straal a. Dit geeft na wat berekeningen:

    \[(x^2+y^2-r^2)^2=a^2[(x-r)^2+y^2]\]

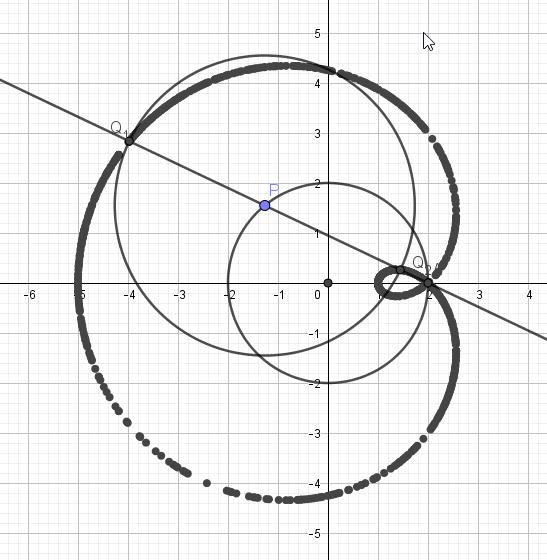
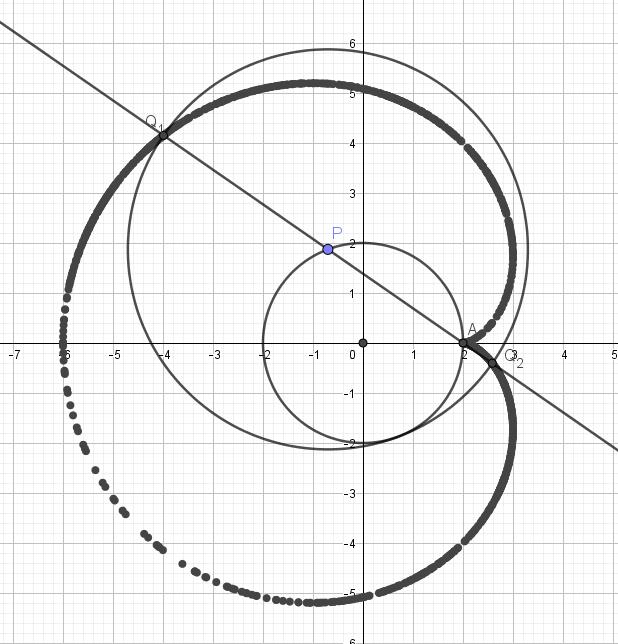
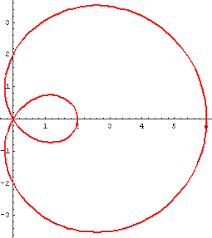
Met Geogebra krijgen we 3 constructies:

  1. Als a<2r: 
  2. Als a=2r, dan krijgen we de cardioïde:
  3. Als a>2r: 

Deze kromme, de Limaçon van Pascal, wordt genoemd naar deFranse jurist en wiskundige Etienne Pascal ( 1588-1651), de vader van, de ons meer bekende, Blaise Pascal. Vroeger onderzoek werd reeds gedaan door Dürer. De naam werd gegeven door Gilles  de Roberval. Limaçon is het Franse woord voor ‘slak’.