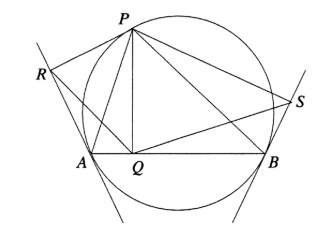
AB is een koorde en P een willekeurig punt van een gegeven cirkel. Q is de loodrechte projectie van P op AB en R en S zijn de loodrechte projecties van P op de raaklijnen aan de cirkel in A en B. Bewijs dat PQ het meetkundig gemiddelde is van PR en PS.

Antwoord

Maken we eerst een tekening:
We proberen aan te tonen dat de driehoeken PRQ en PQS gelijkvormig zijn, want dan is $\dfrac{PR}{PQ}=\dfrac{PQ}{PS}$ en hieruit volgt het gestelde.
De vierhoeken PRAQ en PQSB zijn koordenvierhoeken omdat twee overstaande hoeken recht zijn.
In de eerste koordenvierhoek is $\widehat{PRQ}=\widehat{PAQ}$ omdat in een koordenvierhoek de hoek tussen een zijde en de diagonaal gelijk is aan de hoek gevormd door de overstaande zijde en de andere diagonaal. Daarom is ook $\widehat{PQS}=\widehat{PBS}$ .
Maar de hoeken $\widehat{PAQ}$ en $\widehat{PBS}$ zijn gelijk als hoeken op eenzelfde boog in de gegeven cirkel. Bijgevolg is $\widehat{PRQ}=\widehat{PQS}$ .
Via een analoge redenering is ook $\widehat{PQR}=\widehat{PSQ}$ en dus zijn de driehoeken PRQ en PQS gelijkvormig, zoals gevraagd.